(자바) 서브루틴. 재귀.

프로시저 또는 함수는 그 안에 다른 프로시저에 대한 호출을 포함할 수 있습니다. 포함하여 서브루틴은 자신을 호출할 수 있습니다. 이 경우 컴퓨터는 상관하지 않습니다. 또한 언제나처럼 위에서 아래로 만난 명령을 일관되게 실행합니다.

수학을 기억한다면 그곳에서 수학적 귀납법의 원리를 만날 수 있습니다. 다음과 같습니다.

일부 진술은 모든 자연적인n if
에 대해 참입니다.     1. n = 1 및
    2. 임의의 자연 n = k 에 대한 진술의 타당성으로부터 n = k+1.

프로그래밍에서 이 기술을 재귀
라고 합니다.
재귀는 주어진 간단한 기본 사례를 기반으로 집합 자체의 관점에서 개체 집합을 정의하는 방법입니다.

재귀는 자신을 직접 호출하거나 다른 절차 및 함수를 통해 호출하는 절차(함수)라고도 합니다.
재귀 절차의 예: 정적 무효 Rec(int a) { if (a>0) Rec(a-1); cout << ㅏ; } 도식적으로 재귀 작업은 순서도로 나타낼 수 있습니다.

 

Rec() 프로시저는 매개변수 3으로 실행됩니다. 그런 다음 매개변수 3으로 프로시저 내에서 매개변수 2로 프로시저가 호출되는 식으로 매개변수 0으로 프로시저가 호출될 때까지 계속됩니다. 매개변수 0이 호출되면 재귀 호출은 이미 발생하지 않으며 매개변수 0이 있는 프로시저는 숫자 0을 인쇄하고 종료됩니다. 그런 다음 매개변수 1이 있는 프로시저로 제어가 다시 전송되고 숫자 1을 인쇄하여 작업을 마치는 식입니다. 매개변수 3이 있는 프로시저 전에. 

호출된 모든 프로시저는 작업이 완료될 때까지 메모리에 저장됩니다. 동시 프로시저의 수를 재귀 깊이라고 합니다.

우리는 재귀가 서브루틴에 포함된 명령을 반복적으로 실행하는 것을 보았습니다. 그리고 이것은 차례로 사이클의 작업과 유사합니다. Prolog와 같이 루프 구성이 전혀 없는 프로그래밍 언어가 있습니다. 
for 루프의 작동을 시뮬레이션해 봅시다. 
for 루프에는 단계 카운터 변수가 포함되어 있습니다. 재귀 서브루틴에서 이러한 변수는 매개변수로 전달될 수 있습니다. //두 개의 매개변수가 있는 LoopImitation() 프로시저 //첫 번째 매개변수 – 걸음 수 카운터, 두 번째 매개변수 – 총 단계 수 무효 LoopImitation(int i, int n) { cout << "안녕 엔" << 나는 << 끝; // i의 모든 값에 대해 반복되는 연산자 if (i < n) //루프 카운터가 값 n과 같을 때까지, { // i+1 매개변수를 사용하여 프로시저의 새 인스턴스를 호출합니다(다음 i 값으로 이동). LoopImitation(i+1, n); } }

반복 프로그래밍 — 넓은 의미에서 – 자체 호출로 이어지지 않고 작업이 여러 번 반복되는 데이터 처리 조직(  %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursion" >재귀). 좁은 의미에서 — 한 단계 순환 데이터 처리 프로세스. 
종종 현재 단계(반복)의 반복 알고리즘은 이전 단계에서 계산된 동일한 작업 또는 작업의 결과를 사용합니다.  이러한 계산의 한 예는 순환 관계의 계산입니다. 
재귀 값의 간단한 예는 계승입니다. \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \ \cdot N\) 각 단계(반복)에서의 값 계산은 \(N=N \cdot i\) 입니다.  \(N\) 값을 계산할 때 이미 저장된 값\(N\).< br />
숫자의 계승은 반복 공식을 사용하여 설명할 수도 있습니다.



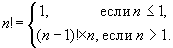
이 설명이 재귀 함수에 불과하다는 것을 알 수 있습니다.
여기서 첫 번째 줄(\(n <= 1\)) — 이것은 기본 케이스(재귀의 종료 조건)이고 두 번째 줄은 다음 단계로의 전환입니다. 
  <몸>
함수 호출에는 약간의 추가 오버헤드가 포함되므로 비재귀 요인 계산이 약간 더 빠릅니다. 
결론: 재귀 없이 간단한 반복 알고리즘으로 프로그램을 작성할 수 있는 경우 재귀 없이 작성해야 합니다. 그러나 여전히 계산 프로세스가 재귀에 의해서만 구현되는 많은 종류의 문제가 있습니다.
반면에 재귀 알고리즘은 종종 더 이해하기 쉽습니다.
 

재귀 계승 함수는 다음과 같습니다.	일반적인 비재귀적 방식으로 계승을 찾는 알고리즘 비교
int 팩토리얼(int n){ if (n > 1) return n * 계승(n - 1); 그렇지 않으면 1을 반환합니다. }	x = 1; for (i = 2; i <= n; i++) x = x * i; printf("%d",x);
다음 정보가 유용할 수 있습니다. 영문자 '\(A\)' 코드 65 입장 \(char \ c = 65;\) 변수 \(c\) \(A\)  따라서 코드로 원하는 문자를 얻을 수 있습니다. Training problem 숫자를 16진법으로