Daripada hanya mengira cincang jujukan, kita boleh menyimpan nilai pada setiap awalannya. Ambil perhatian bahawa ini akan menjadi nilai cincang untuk jujukan yang sama dengan awalan yang sepadan.
Dengan struktur sedemikian, anda boleh mengira nilai cincang dengan cepat untuk mana-mana subsegmen jujukan ini (serupa dengan jumlah awalan).
Jika kita ingin mengira cincang subsegmen [l;r], maka kita perlu mengambil cincang pada awalan r dan tolak cincang pada awalan l-1 didarab dengan p kepada kuasa r-l+1. Mengapa ini menjadi jelas jika anda menulis nilai pada awalan dan melihat apa yang berlaku. Saya harap anda berjaya melihat gambar ini.
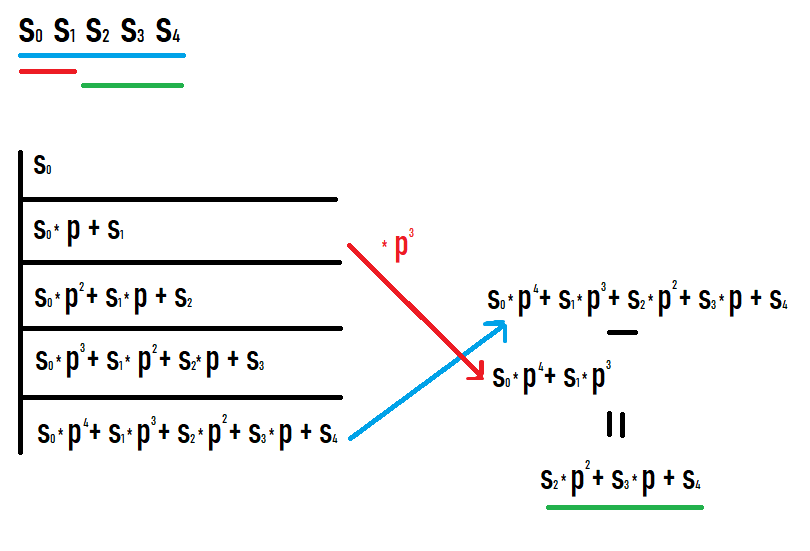
Hasil daripada tindakan sedemikian, kami mendapat cincang subsegmen daripada jujukan asal. Selain itu, cincang ini adalah sama dengan cincangan jika ia dianggap sebagai cincang daripada jujukan yang sama dengan subsegmen ini (tiada penukaran tambahan darjah atau seumpamanya diperlukan untuk dibandingkan dengan nilai lain).
Terdapat dua perkara yang perlu dijelaskan di sini:
1) Untuk mendarab dengan cepat dengan p kepada kuasa r-l+1, adalah perlu untuk mengira awal semua kuasa yang mungkin bagi mod modulo p.
2) Perlu diingat bahawa kami melakukan semua pengiraan modulo modulo, dan oleh itu mungkin ternyata selepas menolak cincang awalan, kami akan mendapat nombor negatif. Untuk mengelakkan ini, anda sentiasa boleh menambah mod sebelum menolak. Juga, jangan lupa untuk mengambil nilai modulo selepas pendaraban dan semua penambahan.
Dalam kod ia kelihatan seperti ini:
#include <bits/stdc++.h>
menggunakan ruang nama std;
typedef long longll;
const int MAXN = 1000003;
// modul asas dan cincang
ll p, mod;
// awalan cincang dan eksponen p
h[MAXN], pows[MAXN];
// mengira cincangan subsegmen [l;r]
ll get_segment_hash(int l, int r) {
pulangan (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int utama()
{
// entah bagaimana dapatkan p dan mod
// prakira kuasa p
pows[0] = 1;
untuk (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// penyelesaian masalah utama
//
pulangan 0;
}