Problem
Labah-labah dan labah-labah terapung di tasik pada dua dahan. Mereka tidak boleh berenang, jadi mereka hanya boleh bertemu apabila dahan bersentuhan.
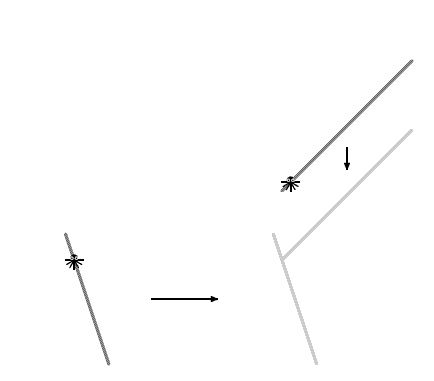
Dengan mengandaikan bahawa cabang adalah dalam bentuk segmen, dan mereka berenang pada kelajuan tetap, tentukan berapa lama masa yang diperlukan untuk bertemu dengan arthropod yang malang itu.
Input
Fail input mengandungi 12 nombor: x1, y1, x2, y2, x 3, y3, x4, y4, v1x, v 1y, v2x, v2y. Koordinat bucu segmen pertama: (x1, y1) dan (x2, y2), menyelaras bucu segmen kedua: (x3, y3) dan (x4, y4< /sub>), kelajuan segmen pertama (v1x, v1y), kelajuan segmen kedua (v2x, v2y). Semua nombor adalah integer dan tidak melebihi 104 dalam nilai mutlak. Pada saat permulaan masa, cawangan tidak bersentuh. Cawangan dijamin mempunyai panjang bukan sifar.
Output
Output dalam fail output masa sehingga detik terdekat apabila cawangan menyentuh, dengan ralat tidak lebih daripada 10
&tolak;4. Jika cawangan tidak pernah menyentuh, cetak nombor -1.
| Input |
Output |
|
0 0 -1 3
4 4 7 7
3 0
0 -1
|
1.6 |
|
0 0 -1 3
4 4 7 7
10
0 -3
|
-1 |
Olimpik Pasukan, Kejohanan Pengaturcaraan Pasukan Murid Sekolah St. Petersburg, 2006, Masalah E