Module: Carian ternary


Problem

9 /9


Carian ternary bersarang bersarang: Penyelamat Angkasa

Problem

Terdapat n planet dalam galaksi, setiap satu daripadanya didiami oleh banyak makhluk hidup yang berbeza. Dan setiap daripada mereka boleh menghadapi masalah! Penyelamat angkasa sedar akan perkara ini dan sentiasa bersedia untuk membantu sesiapa sahaja yang benar-benar memerlukan bantuan ini. Anda hanya perlu menelefon.
 
Penyelamat angkasa kini merancang untuk membina pangkalan menyelamat terbesar dalam sejarah galaksi, tetapi lokasi pangkalan masa hadapan masih belum ditentukan. Memandangkan bantuan kadang-kadang diperlukan dengan segera, penyelamat berusaha untuk mencari titik di galaksi yang memungkinkan untuk sampai ke planet paling jauh dalam masa yang sesingkat mungkin. Dalam erti kata lain, adalah perlu untuk mencari titik sedemikian di angkasa supaya jarak darinya ke planet yang paling jauh daripadanya adalah yang terkecil dari semua titik yang mungkin di angkasa. Malangnya, mereka tidak dapat menyelesaikan masalah sedemikian.
 
Oleh kerana jarak planet yang agak jauh, ia boleh dianggap sebagai titik dalam ruang 3D Euclidean. Jarak antara titik (xi, yi, zi) dan (xj,  yj, zj) dikira dengan formula:
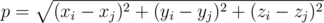
Pangkalan penyelamat boleh ditemui di mana-mana titik di angkasa, termasuk kebetulan dengan mana-mana planet.
 
Galaksi berada dalam bahaya! Menyelamatkan penyelamat angkasa lepas dan arahkan mereka ke titik yang dikehendaki.
 
Input
Baris pertama fail input mengandungi integer n — bilangan planet (1 ≤ N ≤ 100). Setiap baris n seterusnya mengandungi maklumat tentang planet. ke-i baris ini mengandungi tiga integer xi, yi, zi — koordinat planet ke-i ( - 104 ≤ xi, yi, zi ≤ 104, 1.thinsp;≤ i ≤ n). Tiada dua planet yang sama.
 
Output
Dalam baris pertama fail output, cetak tiga nombor nyata yang dipisahkan ruang x0, y0, z0 — koordinat asas. Jika terdapat beberapa penyelesaian, maka ia dibenarkan untuk mencetak mana-mana satu. Jawapan akan dikira jika jarak dari titik ini ke planet paling jauh berbeza daripada keputusan juri dengan tidak lebih daripada 10-6 dalam nilai mutlak atau relatif.
 
 

time 1000 ms
memory 256 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Your Program

Attach a file with the source code of the program:

or select a programming language and type your program

Auto

       

Program check result To check the solution of the problem, you need to register or log in!

Input Output
5
5 0 0
-5 0 0
0 3 4
4 -3 0
2 2 -2
 0.000 0.000 0.000