Sisipkan isihan
Isih sisipan (Isih sisipan) — ;algoritma pengisihan di mana unsur-unsur jujukan input dicari satu demi satu, dan setiap elemen masuk baharu diletakkan di tempat yang sesuai antara elemen yang diisih sebelum ini.
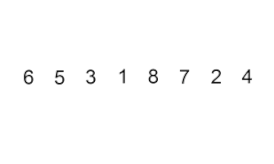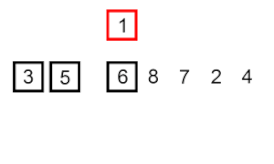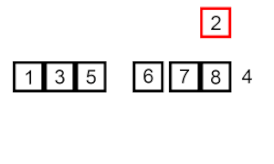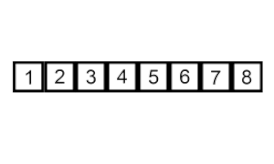
Sisipkan isihan – ia adalah algoritma yang sangat mudah tetapi tidak cekap yang namun mempunyai beberapa kelebihan khusus yang menjadikannya relevan walaupun selepas banyak algoritma lain yang umumnya lebih cekap telah dibangunkan.
Dengan isihan sisipan, anda tidak perlu mempunyai keseluruhan tatasusunan di hadapan sebelum mengisih. Algoritma boleh menerima satu elemen pada satu masa semasa pengisihan. Ini sangat berguna jika kita perlu menambah lebih banyak elemen semasa pengisihan. Algoritma akan memasukkan elemen baharu di tempat yang betul tanpa "melaksanakan semula" mengisih keseluruhan tatasusunan.
Isihan sisipan boleh digunakan dalam amalan kerana kecekapannya pada set data kecil (~10 elemen).
Masalahnya ialah ini: terdapat sebahagian daripada tatasusunan yang telah diisih, dan anda ingin memasukkan unsur-unsur yang tinggal dalam tatasusunan ke dalam bahagian yang diisih, sambil mengekalkan susunan. Untuk melakukan ini, pada setiap langkah algoritma, kami memilih salah satu elemen data input dan memasukkannya pada kedudukan yang dikehendaki dalam bahagian tatasusunan yang telah diisih, sehingga keseluruhan set data input diisih. Kaedah memilih elemen seterusnya daripada tatasusunan input adalah sewenang-wenangnya, tetapi biasanya (dan untuk mendapatkan algoritma pengisihan yang stabil), elemen dimasukkan dalam susunan penampilannya dalam tatasusunan input.
Pelaksanaan algoritma algoritma ini
// Elemen nol dianggap sebagai urutan yang telah diisih.
// Oleh itu, gelung bermula dari 1
LOOP UNTUK I=1 HINGGA N-1 LANGKAH 1
X=A[I]
J=I
APABILA J>0 DAN A[J-1]>X //mencari tempat untuk memasukkan
TUKAR A[J],A[J-1]
J=J-1
TAMATLAH
A[J]=X
SETERUSNYA I
Kerumitan pengiraan: \(\displaystyle O(n^{2})\).