Module: algoritmo de Dijkstra


Problem

1/14

Dijkstra: O Começo (C++)

Theory Click to read/hide

Dado um grafo ponderado direcionado ou não direcionado com n vértices e m arestas. Os pesos de todas as arestas são não negativos. Alguns vértices iniciais são especificados. Você precisa encontrar os comprimentos dos caminhos mais curtos do vértice s para todos os outros vértices e também fornecer uma maneira de imprimir os próprios caminhos mais curtos.
 
Este problema é chamado de "problema de caminho mais curto de fonte única" (problema de caminhos mais curtos de fonte única).

Executa as mesmas tarefas que 1-K BFS, mas sem considerar K. Além disso, como 1-K BFS, ele não lida adequadamente com arestas negativas

Algoritmo:
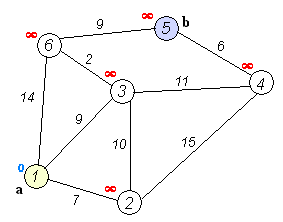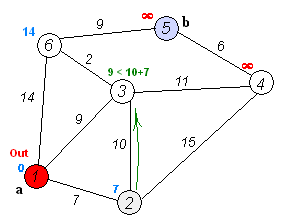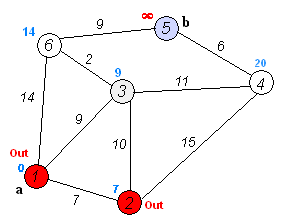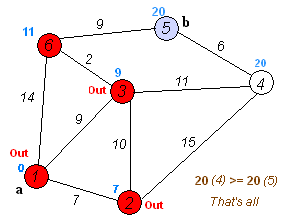
O próprio algoritmo de Dijkstra consiste em N iterações. Na próxima iteração, o vértice V  com a menor distância a ele entre os vértices ainda não marcados, esse vértice se torna marcado e a partir dele ocorrem relaxações de vértices vizinhos.


 o comportamento assintótico final do algoritmo é: O(n2+ m)

Problem

Você recebe um gráfico ponderado direcionado. Encontre a distância mais curta de um dado vértice para outro.
 
Entrada
A primeira linha contém três números: N, S e F (1≤ N≤ 100, 1≤ S, F≤ N), onde N – número de vértices do grafo, S – vértice inicial e F – final. Nas próximas N linhas, insira N números cada, não excedendo 100, – matriz de adjacência de peso do grafo, onde -1 significa nenhuma aresta entre os vértices e qualquer número não negativo – a presença de uma aresta de determinado peso. Os zeros são escritos na diagonal principal da matriz.
 
Saída
É necessário exibir a distância desejada ou -1 se não houver caminho entre os vértices especificados.

Exemplos
# Entrada Saída
1
3 2 1
0 1 1
4 0 1
2 1 0
 3

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
C++
Write the program below 
#include<iostream>
 
using namespace std;
 
int main()
{
    const int N1 = 110;
    int N, S, F, g[N1][N1], i, j, mini, d[N1];
    bool used[N1];
   
    cin >> N >> S >> F;
   
    fill(used, used + N, false);
   
    fill(d, d + N, 10000000);
   
    for (i = 0; i < N; i++)
    {
        for (j = 0; j < N; j++)
            cin >> g[i][j];
    }
   
    d[S - 1] = 0;
   
    for (i = 0; i < N; i++)
    {
        mini = -1;
       
        for (j = 0; j < N; j++)
        {
            if (!used[j] && (mini == -1 || d[j] < d[mini]))
                mini = j;
        }
       
        used[mini] = true; 
    if (d[F - 1] == 10000000)
        cout << "-1";
    else
        cout << d[F - 1];
}

     

Program check result

To check the solution of the problem, you need to register or log in!