Combinações de n elementos por k são compostos que podem ser formados a partir de n elementos, reunindo k elementos em cada ligação; enquanto as conexões diferem umas das outras apenas pelos próprios elementos (a diferença na ordem de seu arranjo não é levada em consideração).
Por exemplo, as seguintes combinações podem ser formadas a partir de 3 elementos (a,b,c)(a,b,c) 2 cada: ab,ac,bc.
O número de todas as combinações possíveis que podem ser formadas de n elementos por k é indicado pelo símbolo

e calculado pela fórmula:
Existem duas maneiras de encontrar o número de combinações

1. Encontre n!, k!, (n – k)! e de acordo com a fórmula acima, calculamos a quantidade, mas a partir de – devido a possível estouro, este método pode ser usado com n <= 12.
2. Com programação dinâmica.
O DP se parecerá com o triângulo de Pascal, com uns no topo e nas arestas, e cada número é igual à soma dos dois números acima dele.
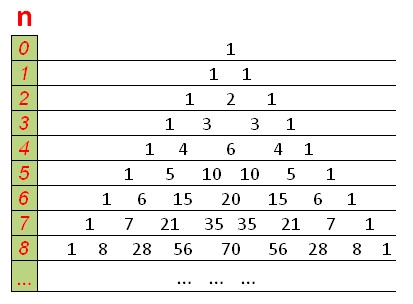
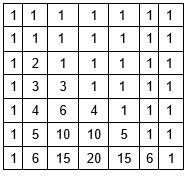
Uma função que conta o número de combinações usando programação dinâmica em O(n ^2):
int C(int n, int k)
{
vector<vector<int> > dp(n + 1, vetor<int>(n + 1, 1)); // Cria um array dp de tamanho (n + 1, n + 1)
para (int i = 0; i <= n; i++) // Preencha a i-ésima linha do array
{
para (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //recalculando (i;j) a posição através de (i - 1; j - 1) e (i - 1; j)
}
}
retorno dp[n][k]; //valor de retorno
}