Problem
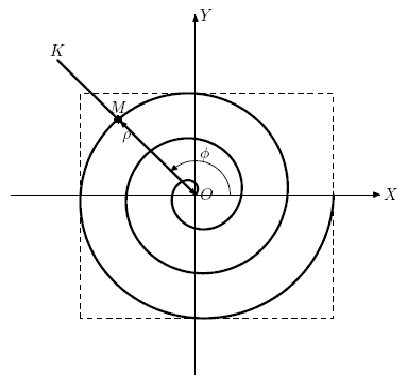
Dima ingressou recentemente no Instituto de Pesquisa de Curvas Planas. Como o nome deste instituto de pesquisa sugere, ele está envolvido em várias pesquisas no campo das curvas planas. Recentemente, o chefe de Dimin, Georgy, encontrou uma curva muito interessante, que, como se descobriu após algumas pesquisas, é conhecida como espiral de Arquimedes. A espiral arquimediana é uma curva plana representando a trajetória do ponto M, que se move uniformemente ao longo do raio OK com origem em O, enquanto o próprio raio OK gira uniformemente em torno do ponto O (veja a figura). Em outras palavras, a distância até a origem ρ = OM linearmente dependente do ângulo de rotação .phi. feixe OK. Neste caso, a rotação do raio OK pelo mesmo ângulo corresponde ao mesmo incremento de distância ρ.
O movimento do ponto M pode ser definido usando vários parâmetros:
• ângulo inicial de rotação .alpha. feixe OK (medido em graus no sentido anti-horário em relação à direção positiva do eixo OX);
• velocidade angular .omega. raio OK (medido em graus por unidade de tempo);
• a distância inicial R do ponto M até a origem (ponto O);
• velocidade V do ponto M ao longo do raio OK.
Se, ao definir esses parâmetros, não limitarmos o tempo de movimento do ponto M, obteremos uma curva infinita, bastante difícil de explorar. Portanto, Dima decidiu limitar-se a estudar alguma parte dessa curva, aquela que é obtida quando o ponto M se move do momento zero do tempo para o momento do tempo T. O problema que Dima resolve é encontrar um retângulo do área mínima com lados paralelos aos eixos coordenados, na qual pode ser inscrito.
Você precisa escrever um programa que encontre o retângulo desejado
Entrada
O arquivo de entrada contém quatro inteiros: ω (1 ≤ omega; ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) e T (1 ≤ T ≤ 1000). Neste problema, assume-se que o ângulo de rotação inicial .alpha. é zero.
Saída
Na primeira linha do arquivo de saída, imprima dois números reais — as coordenadas do canto inferior esquerdo do retângulo desejado e na segunda linha — coordenadas do canto superior direito do retângulo desejado.
A resposta será considerada correta se o valor de cada uma das coordenadas diferir do valor real em não mais que 10-5.
| Entrada |
Saída |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
Team Olympiad, VKOSHP, 2008, Problema I