DFS DFS
A pesquisa em profundidade ( DFS) é um dos principais algoritmos em gráficos. O algoritmo é executado em O(N + M).
Algoritmo
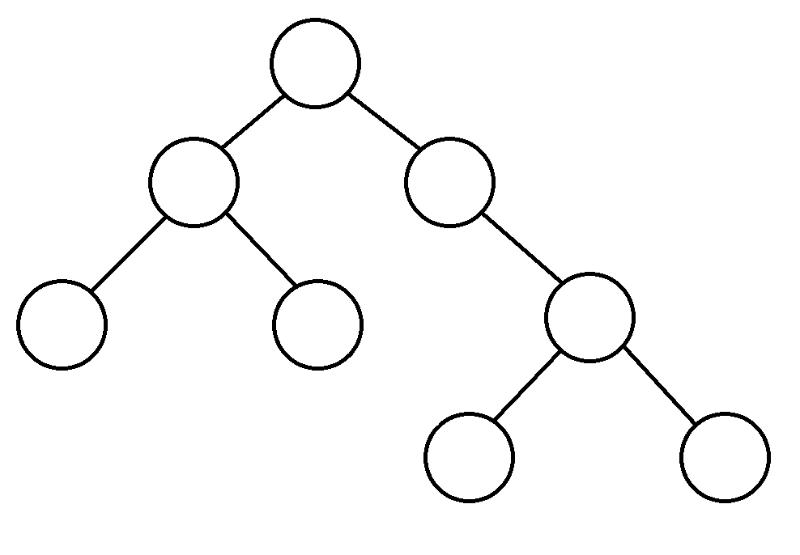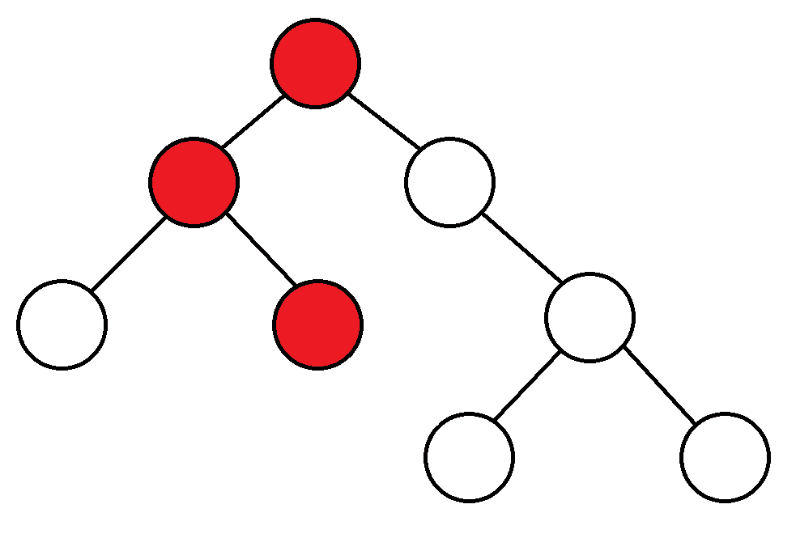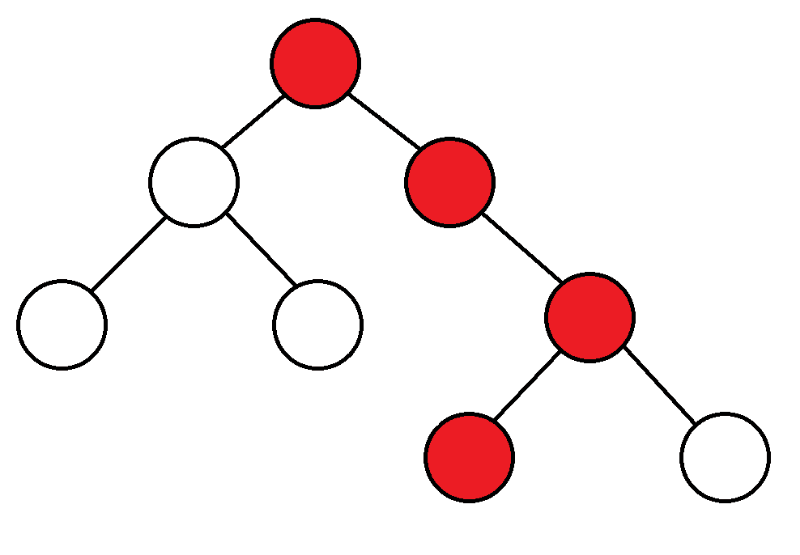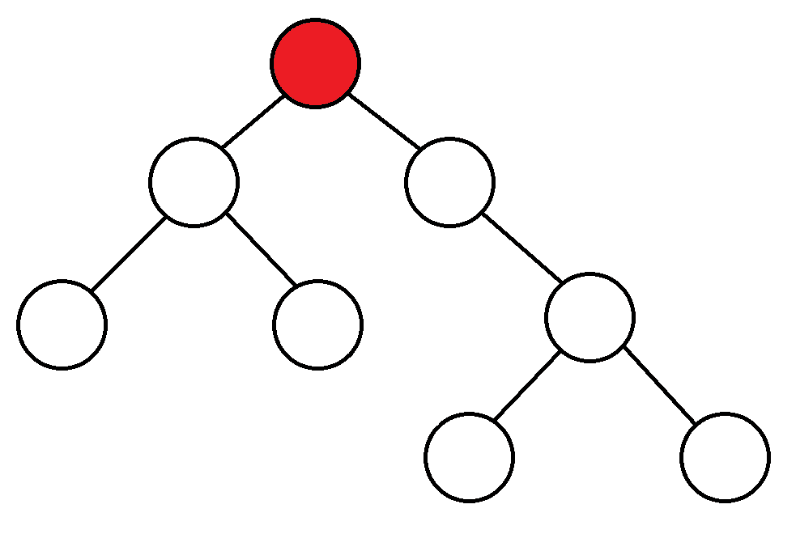
Para começar, começamos do topo, consideramos os filhos deste topo e, se nunca os inserimos, iniciamos o DFS a partir deles.
|
DFS DFS
A pesquisa em profundidade ( DFS) é um dos principais algoritmos em gráficos. O algoritmo é executado em O(N + M).
Algoritmo
Para começar, começamos do topo, consideramos os filhos deste topo e, se nunca os inserimos, iniciamos o DFS a partir deles.

|
Gráfico bipartido
Gráfico bipartido - um gráfico cujos vértices podem ser divididos em dois conjuntos de modo que cada aresta conecte o vértices de diferentes conjuntos.
Freqüentemente, no contexto de grafos bipartidos, o conceito de cores vértices é usado. A divisão de um grafo em duas partes é chamada colorir seus vértices com duas cores diferentes. Cada aresta deve conectar vértices de uma cor diferente.
DFS.
Algoritmo
Começamos a pintar a partir de um vértice arbitrário, que pintamos com uma cor arbitrária.
Ao passar por cada aresta, pinte o próximo vértice na cor oposta.
Se, ao iterar sobre os vértices vizinhos, encontrarmos um vértice já pintado da mesma cor do atual, então há um ciclo ímpar no grafo, o que significa que ele não é bipartido.
|
O algoritmo pode ser descrito da seguinte forma:
Dado um grafo direcionado com n vértices e m arestas. É necessário renumerar seus vértices de forma que cada aresta conduza de um vértice com um número menor para um vértice com um número maior.
Em outras palavras, é necessário encontrar uma permutação de vértices (ordem topológica) correspondente à ordem dada por todas as arestas do grafo.
Usaremos a pesquisa em profundidade (dfs(v))
Se adicionarmos nosso vértice ao início de uma lista no momento da saída de \(dfs(v)\) , então no final nesta lista você obtém uma classificação topológica.
Assim, a ordenação topológica desejada — isso é classificado em ordem decrescente de horários de saída.
|