Module: Genişleyen Ağaçlar: Kruskal'ın Algoritması


Problem

1/4

Kruskal Algoritması: Başlangıç

Theory Click to read/hide

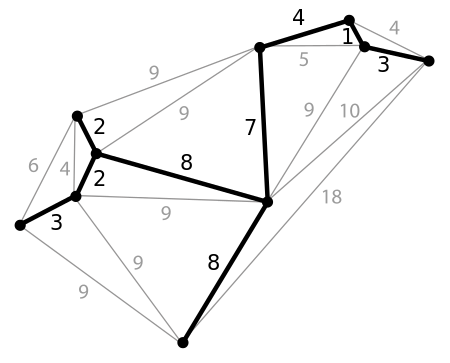
Belirtilen kenar ağırlıklarına sahip bir grafikte minimum yayılan ağaç örneği: 


Kruskal'ın algoritması:

1) Kenarları ağırlığa göre sırala  azalmayan sırada.
2) n ağaçtan oluşan bir liste oluşturuyoruz (her köşe bir ağaçtır).
3)  Bu ağaçları minimum yayılan ağaçta birleştirme sürecini başlatıyoruz:
      tüm kenarlar çaprazlanır ve geçerli kenarın uçları farklı alt ağaçlara aitse bu alt ağaçlar birleştirilir.
4) Tüm kenarların numaralandırılmasının sonunda, tüm köşeler aynı alt ağaca ait olacaktır.

Problem

Bağlantılı bir grafikte minimum ağırlık kapsayan ağaç bulmak gerekir.
 
Giriş verisi biçimi:
 
Girdi dosyasının ilk satırı, sırasıyla grafiğin köşe ve kenarlarının sayısı olan iki doğal sayı N, M içerir. Sonraki m satır, her satırda bir tane olmak üzere kenarların açıklamasını içerir. Kenar sayısı i, sırasıyla kenarın uç noktaları ve ağırlığı olan üç doğal sayı Bi, Ei, Wi ile tanımlanır ( 1 <= B< sub>i, Ei <= N, 0 <= Wi <= 232< /sup>-1.N <= 10, M <= 10).
 
Çıktı biçimi:
 
Çıktı dosyasının tek satırı, minimum yayılan ağacın ağırlığı olan bir doğal sayı içermelidir. 
 

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
C++
Gir Çıktı
4 4
1 2 1
2 3 2
3 4 5
4 1 4
7
Write the program below 
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

struct edge
{
	int l,a,b;
};

bool cmp(const edge &a, const edge &b)
{
    return a.l < b.l;
}

int main()
{
	int m, n;
	cin >> n >> m;

	vector < edge > g(m);

	for (int i = 0; i < m; i++)
	{
		int a, b, l;
		cin >> a >> b >>l;
		edge e;
                e.l = l; e.a= a-1; e.b = b-1;
		g[i] = e;
	}
	long long cost = 0;
	vector < pair<int, int> > res;

	sort(g.begin(), g.end(),cmp);
	vector<int> tree_id(n);
	for (int i = 0; i < n; ++i)
		tree_id[i] = i;
	for (int i = 0; i < m; ++i)
	{
		int a = g[i].a, b = g[i].b, l = g[i].l;
		if (tree_id[a] != tree_id[b])
		{        
			res.push_back(make_pair(a, b));
			int old_id = tree_id[b], new_id = tree_id[a];
			for (int j = 0; j < n; ++j)
				if (tree_id[j] == old_id)
					tree_id[j] = new_id;
		}
	}

	cout << cost;
	return 0;
}

     

Program check result

To check the solution of the problem, you need to register or log in!