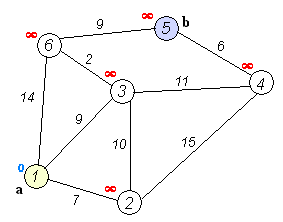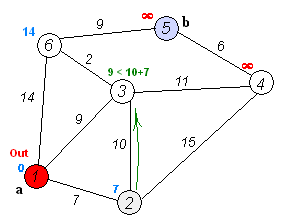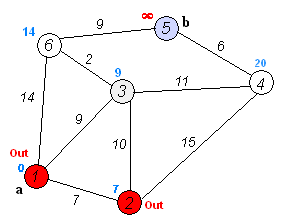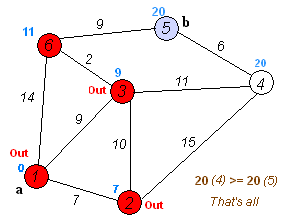
n köşeli ve m kenarlı, yönlü veya yönsüz ağırlıklı bir grafik verildi. Tüm kenarların ağırlıkları negatif değildir. Bazı başlangıç tepe noktaları belirtilmiştir. Köşe noktalarından diğer tüm köşelere giden en kısa yolların uzunluklarını bulmanız ve ayrıca en kısa yolları kendilerinin yazdırması için bir yol sağlamanız gerekir.
Bu soruna "tek kaynaklı en kısa yol sorunu" denir (tek kaynaklı en kısa yollar sorunu).
1-K BFS ile aynı görevleri gerçekleştirir, ancak K'yi dikkate almaz. Ayrıca, 1-K BFS gibi, negatif kenarları düzgün bir şekilde işlemez
Algoritma:
Dijkstra'nın algoritmasının kendisi N yinelemeden oluşur. Bir sonraki yinelemede, tepe noktası V henüz işaretlenmemiş köşelerden ona en küçük mesafe ile, bu köşe işaretlenir ve komşu köşelerde ondan gevşemeler meydana gelir.
algoritmanın nihai asimptotik davranışı: O(n
2+ m)