Sadece bir dizinin karmasını hesaplamak yerine, değeri onun öneklerinin her birinde saklayabiliriz. Bunların, karşılık gelen öneke eşit diziler için hash değerleri olacağını unutmayın.
Böyle bir yapıyla, bu dizinin herhangi bir alt segmenti için hash değerini hızlı bir şekilde hesaplayabilirsiniz (önek toplamlarına benzer).
[l;r] alt segmentinin hash'ini hesaplamak istiyorsak, o zaman r önekinin hash'ini almamız ve l-1 önekindeki hash'i p ile çarpıp r-l+1'in kuvvetini çıkarmamız gerekir. Bunun neden böyle olduğu, öneklere değerleri yazarsanız ve ne olduğunu görürseniz anlaşılır. Umarım bu resme bakmayı başarırsın.
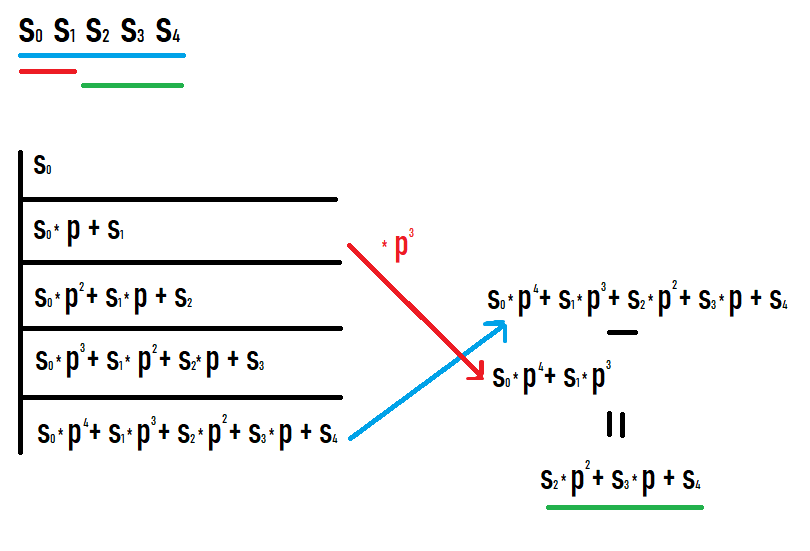
Bu tür eylemlerin bir sonucu olarak, orijinal dizinin bir alt bölümünün bir özetini elde ederiz. Ayrıca, bu karma, bu alt segmente eşit bir diziden bir karma olarak düşünüldüğünde elde edilene eşittir (diğer değerlerle karşılaştırmak için ek derece dönüştürmesi veya benzeri gerekmez).
Burada açıklığa kavuşturulması gereken iki nokta var:
1) p'yi r-l+1 kuvvetiyle hızlı bir şekilde çarpmak için, p modulo modunun olası tüm güçlerini önceden hesaplamak gerekir.
2) Tüm hesaplamaları modulo modulo yaptığımız unutulmamalıdır ve bu nedenle önek karmalarını çıkardıktan sonra negatif bir sayı elde edebileceğimiz ortaya çıkabilir. Bundan kaçınmak için, çıkarmadan önce her zaman mod ekleyebilirsiniz. Ayrıca çarpma ve tüm toplama işlemlerinden sonra modulo değerini almayı unutmayın.
Kodda şöyle görünür:
#include <bits/stdc++.h>
ad alanı std kullanarak;
typedef uzun uzun;
sabit int MAXN = 1000003;
// taban ve hash modülü
l p, mod;
// önek hash ve üsler p
h[MAXN], güçler[MAXN];
// [l;r] alt segmentinin karmasını hesaplıyoruz
get_segment_hash(int l, int r) {
dönüş (h[r] + mod - h[l - 1] * güçler[r - l + 1] % mod) % mod;
}
int ana()
{
// bir şekilde p ve mod al
// güçleri önceden hesapla p
pows[0] = 1;
için (int i = 0; i