Courses

algoritmalar

üçlü arama

Module: üçlü arama

Problem

6 /9

Arşimet sarmalı

Problem

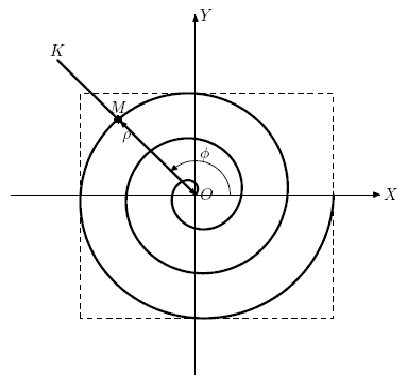
Dima kısa bir süre önce Düz Eğriler Araştırma Enstitüsü'ne katıldı. Bu araştırma enstitüsü adından da anlaşılacağı gibi düzlem eğrileri alanında çeşitli araştırmalar yapmaktadır. Geçenlerde Dimin'in patronu Georgy, bazı araştırmalardan sonra ortaya çıktığı üzere Arşimet sarmalı olarak bilinen çok ilginç bir eğriyle karşılaştı. Arşimet spirali, OK ışını boyunca O'daki orijine sahip düzgün hareket eden M noktasının yörüngesini gösteren bir düzlem eğrisidir, OK ışınının kendisi ise O noktası etrafında düzgün bir şekilde döner (şekle bakın). Başka bir deyişle, orijine olan uzaklık ρ = OM doğrusal olarak dönüş açısına bağlıdır .phi. ışın tamam. Bu durumda, OK ışınının aynı açıyla dönmesi aynı mesafe artışına karşılık gelir ρ.

M noktasının hareketi bir dizi parametre kullanılarak ayarlanabilir:

&boğa; ilk dönüş açısı a. kiriş OK (OX ekseninin pozitif yönüne göre saat yönünün tersine derece olarak ölçülür);

&boğa; açısal hız ray OK (zaman birimi başına derece olarak ölçülür);

&boğa; M noktasından orijine (O noktası) olan ilk R mesafesi;

&boğa; ışın boyunca M noktasının V hızı OK.

Bu parametreleri ayarlayarak M noktasının hareket süresini sınırlamazsak, keşfedilmesi oldukça zor olan sonsuz bir eğri elde ederiz. Bu nedenle Dima, M noktası sıfır anından T anına hareket ettiğinde elde edilen bu eğrinin bir bölümünü incelemekle yetinmeye karar verdi. Dima'nın çözdüğü problem, bir dikdörtgen bulmaktır. çizilebileceği koordinat eksenlerine paralel kenarları olan minimum alan.

İstediğiniz dikdörtgeni bulan bir program yazmanız gerekiyor

Giriş

Giriş dosyası dört tam sayı içerir: ω (1 ≤ omega; ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) ve T (1 ≤ T ≤ 1000). Bu problemde, ilk dönme açısının a olduğu varsayılmaktadır. sıfırdır.

Çıktı

Çıktı dosyasının ilk satırına iki gerçek sayı yazdırın — istenen dikdörtgenin sol alt köşesinin koordinatları ve ikinci satırda — istenen dikdörtgenin sağ üst köşesinin koordinatları.

Koordinatların her birinin değeri gerçek değerden 10-5'ten fazla farklı değilse cevap doğru kabul edilecektir.

Takım Olimpiyatı, VKOSHP, 2008, Problem I

time 1000 ms
memory 256 Mb
Rules for program design and list of errors in automatic problem checking