İkinci dereceden sıralamalar


İkinci dereceden sıralamalar

Sıralama - bir dizinin (listenin) öğelerini belirli bir sırayla yeniden düzenlemedir.

Kabarcık yöntemi (kabarcık sıralama) veya basit değişimlere göre sıralama).
Türün ölümsüz bir klasiği. Eylem ilkesi basit: diziyi baştan sona dolaşıyoruz, aynı anda sıralanmamış komşu öğeleri değiştiriyoruz. Son sıraya ilk geçiş sonucunda "pop up" maksimum eleman. Şimdi dizinin sıralanmamış kısmını (ilk elemandan sondan bir önceki elemana) tekrar atlıyoruz ve yol boyunca sıralanmamış komşuları değiştiriyoruz. İkinci en büyük eleman sondan bir önceki yerde olacaktır. Aynı ruhla devam ederek, dizinin sürekli azalan sıralanmamış kısmını atlayarak bulunan maksimumları sonuna kadar zorlayacağız.
 
Kaynak

Bu algoritmanın algoritmik uygulaması
J=1 İLE N-1 İÇİN DÖNGÜ ADIM 1
   F=0
   I=1 İLE N-J-1 İÇİN DÖNGÜ ADIM 1
     IF A[I] > A[I+1] SONRA
       DEĞİŞİM A[I],A[I+1]
       K=1
   SONRAKİ ben
   IF F=0 THEN EXIT THE LOOP // geçiş sırasında herhangi bir değişim olmadıysa,
  // bu, tüm öğeler anlamına gelir
  //sırayla düzenlenmiş
 SONRAKİ J
Bu algoritmanın karmaşıklığı: \(\displaystyle O(n^{2})\).


Ek yararlı bilgiler: Wikipedia makalesi.

 

Training problem

kabarcık sıralama

Sıralama ekle

Ekleme sıralama (Ekleme sıralama) —  ;girdi dizisinin öğelerinin birer birer arandığı ve her yeni gelen öğenin daha önce sıralanan öğeler arasında uygun yere yerleştirildiği sıralama algoritması.


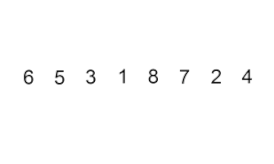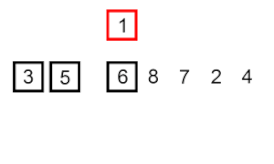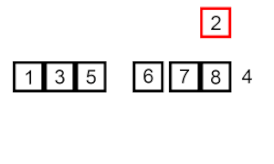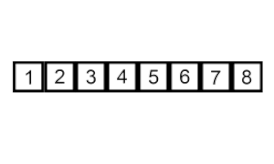
Sıralamayı ekle – çok basit ama verimsiz bir algoritmadır ve yine de genel olarak daha verimli birçok başka algoritma geliştirildikten sonra bile onu alakalı kılan birkaç özel avantaja sahiptir.

Araya eklemeli sıralamada, sıralamadan önce tüm dizinin ön planda olması gerekmez. Algoritma, sıralama sırasında her seferinde bir öğe alabilir. Bu sıralama sırasında daha fazla öğe eklememiz gerekirse çok kullanışlıdır. Algoritma, yeni öğeyi "yeniden çalıştırmadan" doğru yere yerleştirecek tüm diziyi sıralama.

Ekleme sıralaması, küçük (~10 öğeli) veri kümelerindeki verimliliği nedeniyle pratikte kullanılabilir.

Sorun şu ki: dizinin zaten sıralanmış bir kısmı var ve sırayı korurken dizinin geri kalan öğelerini sıralanan kısma eklemek istiyorsunuz. Bunu yapmak için, algoritmanın her adımında, giriş verisi öğelerinden birini seçeriz ve onu, tüm girdi veri seti sıralanana kadar dizinin zaten sıralanmış bölümünde istenen konuma yerleştiririz. Girdi dizisinden bir sonraki öğeyi seçme yöntemi isteğe bağlıdır, ancak genellikle (ve kararlı bir sıralama algoritması elde etmek için), öğeler girdi dizisindeki görünüm sırasına göre eklenir.

Bu algoritmanın algoritmik uygulaması
// Boş öğe zaten sıralanmış bir dizi olarak kabul edilir.
// Bu nedenle, döngü 1'den başlar
I=1 İLE N-1 İÇİN DÖNGÜ ADIM 1
   X=A[I]
   J=ben
   WHEN J>0 AND A[J-1]>X //eklenecek yer aranıyor
     DEĞİŞİM A[J],A[J-1]
     J=J-1
   Güle güle
   A[J]=X
 SONRAKİ ben
Hesaplama karmaşıklığı: \(\displaystyle O(n^{2})\).

Training problem

Ekleme sıralaması