Bir prosedür veya işlev, içindeki başka bir prosedüre çağrı içerebilir. Dahil olmak üzere, alt program kendisini arayabilir. Bu durumda, bilgisayar umursamıyor. Ayrıca, her zaman olduğu gibi, yukarıdan aşağıya tanıştığı komutları tutarlı bir şekilde yürütür.
Matematiği hatırlarsanız, orada matematiksel tümevarım ilkesi ile tanışabilirsiniz. Aşağıdaki gibidir:
bazı ifadeler her doğal n için doğrudur, eğer
1. n = 1 ve için geçerlidir
2. Herhangi bir keyfi doğal n = k için önermenin geçerliliğinden, n = k+1 için doğru olduğu sonucu çıkar.
Programlamada bu tekniğe özyineleme
denir
Yineleme, verilen basit temel durumlara dayalı olarak, bir nesne kümesini kümenin kendisi açısından tanımlamanın bir yoludur.
Tekrarlı kendini doğrudan veya diğer prosedürler ve işlevler aracılığıyla çağıran bir prosedür (işlev) olarak da adlandırılır
Özyinelemeli bir prosedür örneği:
statik geçersiz Rec(int a)
{
eğer (a>0) Rec(a-1);
cout
Şematik olarak, özyineleme işi bir akış şemasıyla temsil edilebilir.
Rec() prosedür parametre 3 ile yürütülür. Ardından, parametre 3 ile prosedür içinde, parametre 2 ile prosedür çağrılır ve parametre 0 ile prosedür çağrılana kadar böyle devam eder. 0 parametresi çağrıldığında, özyinelemeli çağrı zaten gerçekleşmeyecek ve 0 parametresiyle yapılan prosedür 0 sayısını yazdıracak ve sonlandırılacaktır. Daha sonra kontrol 1 parametresi ile prosedüre geri aktarılır, o da 1 sayısını yazdırarak işini bitirir ve bu böyle devam eder. parametre 3 ile prosedürden önce.
Çağrılan tüm prosedürler, işlerini tamamlayana kadar hafızada saklanır. Eşzamanlı prosedürlerin sayısı tekrarlama derinliği olarak adlandırılır.
|
Özyinelemenin, bir alt programda içerilen talimatların tekrar tekrar yürütülmesi olduğunu gördük. Ve bu da döngünün çalışmasına benzer. Döngü yapısının hiç bulunmadığı programlama dilleri vardır, örneğin Prolog.
For döngüsünün işleyişini simüle etmeye çalışalım.
For döngüsü bir adım sayacı değişkeni içerir. Özyinelemeli bir alt programda, böyle bir değişken parametre olarak iletilebilir.
//LoopImitation() iki parametreli prosedür
//İlk parametre – adım sayacı, ikinci parametre – toplam adım sayısı
geçersiz LoopImitation(int i, int n)
{
cout
|
Yinelemeyi anlamak için yinelemeyi anlamanız gerekir...
Yineleme programlamada — geniş anlamda — eylemlerin kendilerine çağrılara yol açmadan birçok kez tekrarlandığı veri işleme organizasyonu (%BA%D1%83%D1%80%D1%81%D0%B8%D1%8F'den farklı olarak) title="Tekrarlama" >Yinelemeler). Dar anlamda — tek adımlı döngüsel veri işleme süreci.
Genellikle geçerli adımdaki (yineleme) yinelemeli algoritmalar, önceki adımlarda hesaplanan aynı işlemin veya eylemin sonucunu kullanır. Bu tür hesaplamalara bir örnek, yineleme ilişkilerinin hesaplanmasıdır.
Özyinelemeli değerin basit bir örneği faktöriyeldir: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \\cdot N\)
Her adımda (yineleme) değerin hesaplanması şu şekildedir: \(N=N \cdot i\) . \(N\) değerini hesaplarken, önceden depolanmış değeri \(N\) alırız >.
Bir sayının faktöriyeli yinelenen formül kullanılarak da açıklanabilir:
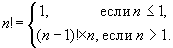
Bu açıklamanın özyinelemeli bir işlevden başka bir şey olmadığını fark edebilirsiniz.
İşte ilk satır ( \(n <= 1\)) — bu temel durumdur (yinelemenin bitiş koşulu) ve ikinci satır bir sonraki adıma geçiştir.
| Özyinelemeli faktöriyel işlevi şuna benzer |
Faktöriyeli bulmak için algoritmayı yinelemeli olmayan şekilde karşılaştırın |
|
int Faktöriyel(int n){
eğer (n > 1)
dönüş n * Faktöriyel(n - 1);
aksi takdirde 1 döndürür;
}
|
x = 1;
için (i = 2; i <= n; i++)
x = x * ben;
printf("%d",x);
|
İşlev çağrılarının bazı ek yük içerdiği anlaşılmalıdır, bu nedenle özyinelemeli olmayan bir faktöriyel hesaplaması biraz daha hızlı olacaktır.
Sonuç: Basit bir yinelemeli algoritmaya sahip, yinelemesiz bir program yazabileceğiniz yerde, yinelemesiz yazmanız gerekir. Ancak yine de, hesaplama sürecinin yalnızca özyineleme ile uygulandığı geniş bir problem sınıfı vardır.
Öte yandan, özyinelemeli algoritmalar genellikle daha anlaşılırdır.
Bu bilgiyi yararlı bulabilirsiniz:
İngilizce harf '\(A\)' 65 kodu vardır
giriş
\(char \ c = 65;\) bir İngilizce harfi \(c\) \(A\)
Böylece istediğiniz harfi koduna göre alabilirsiniz.
|
|