|
|
Sadece bir dizinin karmasını hesaplamak yerine, değeri onun öneklerinin her birinde saklayabiliriz. Bunların, karşılık gelen öneke eşit diziler için hash değerleri olacağını unutmayın.
Böyle bir yapıyla, bu dizinin herhangi bir alt segmenti için hash değerini hızlı bir şekilde hesaplayabilirsiniz (önek toplamlarına benzer).
[l;r] alt segmentinin hash'ini hesaplamak istiyorsak, o zaman r önekinin hash'ini almamız ve l-1 önekindeki hash'i p ile çarpıp r-l+1'in kuvvetini çıkarmamız gerekir. Bunun neden böyle olduğu, öneklere değerleri yazarsanız ve ne olduğunu görürseniz anlaşılır. Umarım bu resme bakmayı başarırsın.
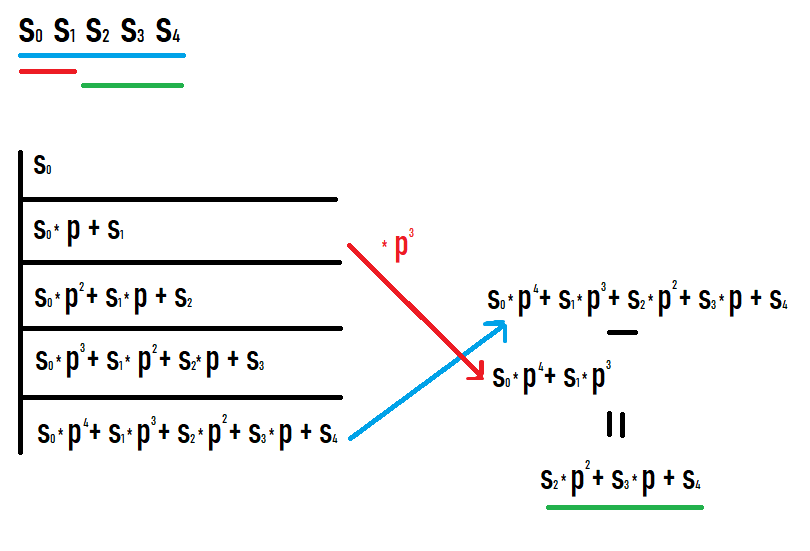
Bu tür eylemlerin bir sonucu olarak, orijinal dizinin bir alt bölümünün bir özetini elde ederiz. Ayrıca, bu karma, bu alt segmente eşit bir diziden bir karma olarak düşünüldüğünde elde edilene eşittir (diğer değerlerle karşılaştırmak için ek derece dönüştürmesi veya benzeri gerekmez).
Burada açıklığa kavuşturulması gereken iki nokta var:
1) p'yi r-l+1 kuvvetiyle hızlı bir şekilde çarpmak için, p modulo modunun olası tüm güçlerini önceden hesaplamak gerekir.
2) Tüm hesaplamaları modulo modulo yaptığımız unutulmamalıdır ve bu nedenle önek karmalarını çıkardıktan sonra negatif bir sayı elde edebileceğimiz ortaya çıkabilir. Bundan kaçınmak için, çıkarmadan önce her zaman mod ekleyebilirsiniz. Ayrıca çarpma ve tüm toplama işlemlerinden sonra modulo değerini almayı unutmayın.
Kodda şöyle görünür:
#include <bits/stdc++.h>
ad alanı std kullanarak;
typedef uzun uzun;
sabit int MAXN = 1000003;
// taban ve hash modülü
l p, mod;
// önek hash ve üsler p
h[MAXN], güçler[MAXN];
// [l;r] alt segmentinin karmasını hesaplıyoruz
get_segment_hash(int l, int r) {
dönüş (h[r] + mod - h[l - 1] * güçler[r - l + 1] % mod) % mod;
}
int ana()
{
// bir şekilde p ve mod al
// güçleri önceden hesapla p
pows[0] = 1;
için (int i = 0; i
|
A dizesinin hA 'ya eşit bir hash'i ve B dizesinin hB'ye eşit bir hash'i varsa, o zaman AB dizesinin hash'ini hızlıca hesaplayabiliriz:
hAB = hA * p|B| + hB <- her şeyi sayma modulo
nerede |B| - B dizisinin uzunluğu.
|
Sekanslara ek olarak, kümeleri de karma yapabilirsiniz. Yani, üzerinde herhangi bir düzen olmayan nesne kümeleri. Aşağıdaki formüle göre hesaplanır:
hash(A) = \(\sum_{a \in A} p^{ord(a)}\) <- her şeyi sayma modulo
burada ord, kümenin bir nesnesine tüm olası nesneler arasında mutlak sıra sayısını atayan bir işlevdir (örneğin, nesneler doğal sayılarsa, o zaman ord(x) = x ve küçük Latin harfleri ise o zaman ord(& #39;a') = 1, sıra('b') = 2 vb.)
Yani, her nesne için, bu nesnenin sayısının gücüne tabana eşit bir değer ilişkilendiririz ve tüm kümenin bir karmasını elde etmek için tüm bu değerleri toplarız. Formülden de anlaşılacağı gibi, kümeye bir öğe eklenirse veya kümeden çıkarılırsa (sadece gerekli değeri ekleyin veya çıkarın) hash kolayca yeniden hesaplanır. Aynı mantık, tek öğeler eklenmez veya kaldırılmazsa, ancak diğer kümeler eklenirse (sadece hashlerini ekleyin / çıkarın).
Zaten anlayabileceğiniz gibi, tek öğeler, hash'i hesaplayabileceğimiz 1 boyutlu kümeler olarak kabul edilir. Ve daha büyük kümeler, bu tür tekli kümelerin bir birleşimidir; burada kümeleri birleştirerek hashlerini ekleriz.
Aslında, bu hala aynı polinom hash'idir, ancak pm 'deki katsayıdan önce şu değere sahibiz: dizi elemanının n - m - 1 (burada n, dizinin uzunluğudur) ve şimdi bu, kümedeki mutlak sıra numarası m'ye eşit olan öğelerin sayısıdır.
Bu tür karmada, kişi yeterince büyük bir taban almalı (maksimum küme boyutundan daha büyük) veya mutlak sıra numarası m olan bir p nesnesi kümesinin, mutlak sıra numarası olan bir nesneli bir kümeyle aynı karma değerine sahip olduğu durumlardan kaçınmak için çift karma kullanmalıdır. sıra numarası m+1.
|
Köklü ağaçları verimli bir şekilde hashlemenin çeşitli yolları da vardır.
Bu yöntemlerden biri şu şekilde düzenlenmiştir:
Köşeleri derinlemesine geçiş sırasına göre yinelemeli olarak işleriz. Tek bir köşenin hash değerinin p'ye eşit olduğunu varsayacağız. Çocuklu köşeler için önce onlar için algoritmayı çalıştırırız, ardından çocuklar aracılığıyla mevcut alt ağacın karmasını hesaplarız. Bunu yapmak için, alt ağaçların hashlerini bir sayı dizisi olarak düşünün ve hash'i bu diziden hesaplayın. Bu, mevcut alt ağacın karması olacaktır.
Çocuklardaki sıra bizim için önemli değilse, hash'i hesaplamadan önce alt ağaçlardan hash sırasını sıralarız ve ardından sıralanan diziden hash'i hesaplarız.
Bu şekilde, ağaçların izomorfizmini kontrol edebilirsiniz - çocuklar üzerinde sıra olmadan sadece hash'i sayın (yani, her seferinde çocukların hash'lerini sıralayarak). Ve eğer köklerin hash'leri eşleşirse, ağaçlar izomorfiktir, aksi halde değildir.
Köksüz ağaçlar için her şey benzer şekilde gerçekleşir, ancak ağırlık merkezi kök olarak alınmalıdır. Veya iki merkez varsa, bir çift karma düşünün.
|