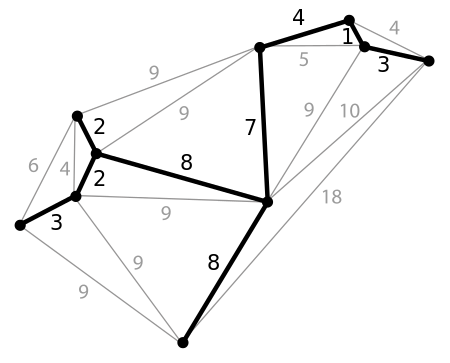
Ví dụ về cây bao trùm tối thiểu trong biểu đồ có trọng số cạnh được chỉ định:
Thuật toán Kruskal:
1) Sắp xếp các cạnh theo trọng lượng theo thứ tự không giảm.
2) Lập danh sách n cây (mỗi đỉnh là một cây).
3) Chúng tôi bắt đầu quá trình kết hợp các cây này thành một cây bao trùm tối thiểu:
tất cả các cạnh đều được duyệt qua và nếu các đầu của cạnh hiện tại thuộc về các cây con khác nhau, thì các cây con này sẽ được hợp nhất.
4) Khi kết thúc phép liệt kê tất cả các cạnh, tất cả các đỉnh sẽ thuộc về cùng một cây con.