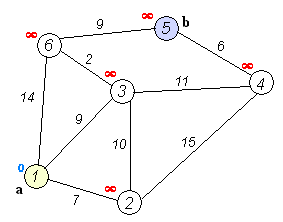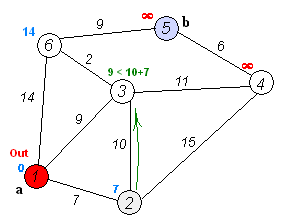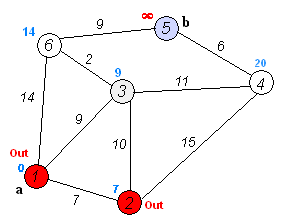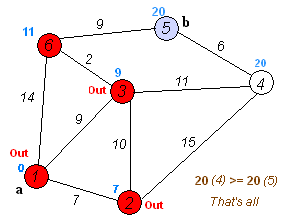
Cho một đồ thị có trọng số có hướng hoặc vô hướng có n đỉnh và m cạnh. Trọng số của tất cả các cạnh là không âm. Một số đỉnh bắt đầu s được chỉ định. Bạn cần tìm độ dài của các đường đi ngắn nhất từ đỉnh s đến tất cả các đỉnh khác, đồng thời cung cấp cách tự in các đường đi ngắn nhất.
Vấn đề này được gọi là "vấn đề đường dẫn ngắn nhất nguồn đơn" (vấn đề đường đi ngắn nhất từ một nguồn).
Thực hiện các tác vụ giống như 1-K BFS, nhưng không liên quan đến K. Ngoài ra, giống như 1-K BFS, nó không xử lý đúng các cạnh âm
Thuật toán:
Bản thân thuật toán Dijkstra bao gồm N lần lặp. Ở lần lặp tiếp theo, đỉnh V với khoảng cách nhỏ nhất đến nó trong số các đỉnh chưa được đánh dấu, đỉnh này sẽ được đánh dấu và các đỉnh lân cận xảy ra từ nó.
hành vi tiệm cận cuối cùng của thuật toán là: O(n
2+ m)