Hỗn hợp của n phần tử bởi k là hợp chất có thể tạo thành từ n phần tử, thu k phần tử trong mỗi liên kết; trong khi các kết nối khác nhau chỉ bởi chính các phần tử (sự khác biệt về thứ tự sắp xếp của chúng không được tính đến).
Ví dụ: các kết hợp sau có thể được tạo từ 3 phần tử (a,b,c)(a,b,c) 2 mỗi phần tử: ab,ac,bc.
Số lượng tất cả các kết hợp có thể được tạo thành từ n phần tử bởi k được biểu thị bằng ký hiệu

và được tính theo công thức:
Có hai cách để tìm số lượng kết hợp

1. Tìm n!, k!, (n – k)! và theo công thức trên, chúng tôi tính toán số lượng, nhưng từ – do có thể tràn, phương pháp này có thể được sử dụng với n <= 12.
2. Với lập trình động.
DP sẽ giống như tam giác Pascal, với các số ở trên cùng và các cạnh, và mỗi số bằng tổng của hai số ở trên nó.
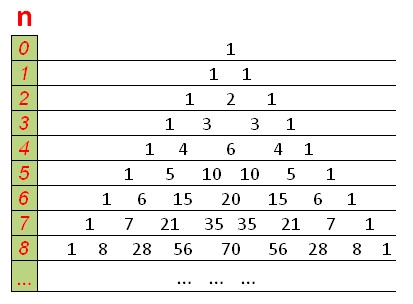
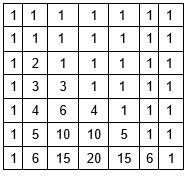
Hàm đếm số lượng kết hợp sử dụng lập trình động trong O(n^2 ):
int C(int n, int nhịp > k)
{
vectơ<vector<int> > dp(n + 1, vector<int>(n + 1, 1)); // Tạo mảng dp có kích thước (n + 1, n + 1)
cho (int i = 0; i <= n; i++) // Điền vào dòng thứ i của mảng
{
cho (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //tính lại vị trí (i;j) qua (i - 1; j - 1) và (i - 1; j)
}
}
return dp[n][k]; //giá trị trả về
}