Thay vì chỉ tính toán hàm băm của một chuỗi, chúng ta có thể lưu trữ giá trị tại mỗi tiền tố của nó. Lưu ý rằng đây sẽ là các giá trị băm cho các chuỗi bằng tiền tố tương ứng.
Với cấu trúc như vậy, bạn có thể nhanh chóng tính toán giá trị băm cho bất kỳ phân đoạn con nào của chuỗi này (tương tự như tổng tiền tố).
Nếu chúng ta muốn tính hàm băm của phân đoạn con [l;r], thì chúng ta cần lấy hàm băm trên tiền tố r và trừ hàm băm trên tiền tố l-1 nhân với p thành lũy thừa của r-l+1. Tại sao điều này trở nên rõ ràng nếu bạn viết các giá trị trên các tiền tố và xem điều gì sẽ xảy ra. Tôi hy vọng bạn thành công khi nhìn vào bức tranh này.
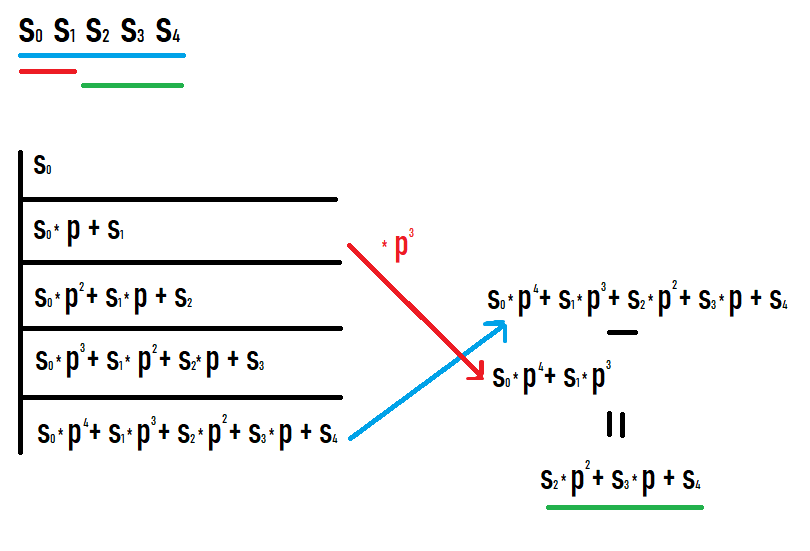
Kết quả của những hành động như vậy, chúng tôi nhận được một hàm băm của một phân đoạn con của chuỗi ban đầu. Ngoài ra, giá trị băm này bằng với giá trị đó nếu nó được coi là giá trị băm từ một chuỗi tương đương với phân đoạn con này (không cần chuyển đổi thêm độ hoặc tương tự để so sánh với các giá trị khác).
Ở đây có hai điểm cần làm rõ:
1) Để nhân nhanh lũy thừa r-l+1 với p, cần phải tính toán trước tất cả các lũy thừa có thể có của p modulo mod.
2) Cần phải nhớ rằng chúng tôi thực hiện tất cả các phép tính modulo modulo, và do đó, có thể xảy ra rằng sau khi trừ các giá trị băm tiền tố, chúng tôi sẽ nhận được một số âm. Để tránh điều này, bạn luôn có thể thêm mod trước khi trừ. Ngoài ra, đừng quên lấy giá trị modulo sau các phép nhân và tất cả các phép cộng.
Trong mã nó trông như thế này:
#include <bits/stdc++.h>
sử dụng không gian tên std;
typedef dài dài;
const int MAXN = 1000003;
// cơ sở và mô-đun băm
sẽ p, mod;
// tiền tố băm và số mũ p
h[MAXN], pows[MAXN];
// tính toán giá trị băm của phân đoạn con [l;r]
sẽ get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int chính ()
{
// bằng cách nào đó lấy p và mod
// tính trước lũy thừa p
pows[0] = 1;
for (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// giải quyết vấn đề chính
//
trả về 0;
}