Một thủ tục hoặc hàm có thể chứa lời gọi đến một thủ tục khác bên trong nó. Bao gồm, chương trình con có thể gọi chính nó. Trong trường hợp này, máy tính không quan tâm. Anh ấy cũng như mọi khi, nhất quán thực hiện các mệnh lệnh mà anh ấy đã gặp từ trên xuống dưới.
Nếu bạn nhớ toán học, thì ở đó bạn có thể gặp nguyên lý quy nạp toán học. Nó như sau:
một số mệnh đề đúng với mọi n tự nhiên nếu
1. nó hợp lệ cho n = 1 và
2. từ tính hợp lệ của mệnh đề đối với bất kỳ n = k tự nhiên tùy ý nào, suy ra nó đúng với n = k+1.
Trong lập trình, kỹ thuật này được gọi là đệ quy
Đệ quy là một cách xác định một tập hợp các đối tượng theo chính tập hợp đó, dựa trên các trường hợp cơ sở đơn giản đã cho.
Đệ quy cũng sẽ được gọi là thủ tục (hàm) gọi chính nó trực tiếp hoặc thông qua các thủ tục và hàm khác
Một ví dụ về thủ tục đệ quy:
void Rec(int a)
{
nếu (a>0) Rec(a-1);
cout << Một;
}
Về mặt sơ đồ, công việc của đệ quy có thể được biểu diễn bằng một sơ đồ
Thủ tục Rec() được thực thi với tham số 3. Sau đó, bên trong thủ tục có tham số 3, thủ tục có tham số 2 được gọi, v.v., cho đến khi thủ tục có tham số 0 được gọi. tham số 0 được gọi, cuộc gọi đệ quy đã có sẽ không xảy ra và thủ tục với tham số 0 sẽ in số 0 và kết thúc. Sau đó, điều khiển được chuyển trở lại quy trình với tham số 1, nó cũng hoàn thành công việc của mình bằng cách in số 1, v.v. trước thủ tục có tham số 3.
Tất cả các thủ tục được gọi được lưu trữ trong bộ nhớ cho đến khi chúng hoàn thành công việc của mình. Số lượng các thủ tục đồng thời được gọi là độ sâu đệ quy.
|
Đệ quy. Mô phỏng vòng lặp
Chúng ta đã thấy rằng đệ quy là việc thực hiện lặp đi lặp lại các lệnh chứa trong một chương trình con. Và điều này, đến lượt nó, tương tự như công việc của chu kỳ. Có những ngôn ngữ lập trình hoàn toàn không có cấu trúc vòng lặp, chẳng hạn như Prolog.
Hãy thử mô phỏng hoạt động của vòng lặp for.
Vòng lặp for chứa một biến đếm bước. Trong chương trình con đệ quy, một biến như vậy có thể được truyền dưới dạng tham số.
// Quy trình LoopImitation() với 2 tham số.
// Tham số đầu tiên – bộ đếm bước, tham số thứ hai – tổng số bước.
void LoopImitation(int i, int n)
{
cout << "Xin chào N" << tôi << kết thúc; // Toán tử được lặp lại với bất kỳ giá trị nào của i
if (i < n) // Cho đến khi bộ đếm vòng lặp bằng n,
{ // gọi một thể hiện mới của thủ tục, với tham số i+1 (đi tới giá trị tiếp theo i).
LoopImitation(i + 1, n);
}
}
|
Đệ quy và phép lặp
Để hiểu đệ quy, bạn cần hiểu đệ quy...
Lặp lại trong lập trình - một bướccủa quy trình xử lý dữ liệu tuần hoàn.
Thông thường các thuật toán lặp ở bước hiện tại (lặp) sử dụng kết quả của cùng một thao tác hoặc hành động được tính ở các bước trước đó. Một ví dụ về các phép tính như vậy là phép tính các quan hệ lặp lại.
Một ví dụ đơn giản về giá trị đệ quy là giai thừa: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
Phép tính giá trị ở mỗi bước (lặp lại) là \(N=N \cdot i\) . Khi tính giá trị của \(N\), chúng tôi lấy giá trị đã được lưu trữ \(N\).
Giai thừa của một số cũng có thể được mô tả bằng cách sử dụng công thức truy hồi:
\(\begin{equation*} n!= \begin{cases} 1 &\text{n <= 1,}\\ (n-1)! \cdot n &\text{n > 1.} \end{cases} \end{equation*}\)
Bạn có thể nhận thấy rằng mô tả này không gì khác hơn là một hàm đệ quy.
Ở đây, dòng đầu tiên ( \(n <= 1\)) là trường hợp cơ sở (điều kiện kết thúc đệ quy) và dòng thứ hai là chuyển tiếp sang bước tiếp theo.
| Hàm giai thừa đệ quy |
Thuật toán lặp |
|
int Giai thừa(int n)
{
nếu (n > 1)
trả về n * Giai thừa (n - 1);
khác trả lại 1;
}
|
x = 1;
cho (i = 2; i <= n; i++)
x = x * i;
cout << x;
|
Bạn nên hiểu rằng các lệnh gọi hàm liên quan đến một số chi phí bổ sung, do đó phép tính giai thừa không đệ quy sẽ nhanh hơn một chút.
Kết luận:chỗ bạn có thể viết chương trình với thuật toán lặp đơn giản, không đệ quy, thì bạn cần viết không đệ quy. Tuy nhiên, có rất nhiều bài toán mà quá trình tính toán chỉ được thực hiện bằng đệ quy.
Mặt khác, thuật toán đệ quy thường dễ hiểu hơn.
Nhiệm vụ
Trong bảng chữ cái ngôn ngữ của bộ tộc "Tumba-Yumba"; bốn chữ cái: "K", "L", "M" và "N". Bạn cần hiển thị tất cả các từ bao gồm n chữ cái có thể được tạo từ các chữ cái trong bảng chữ cái này.
Sự cố này là một sự cố brute-force bình thường có thể được rút gọn thành một sự cố nhỏ hơn.
Chúng ta sẽ lần lượt thay thế các chữ cái cho từ đó.
Vị trí đầu tiên của một từ có thể là một trong 4 chữ cái của bảng chữ cái (K. L, M, N).
Hãy đặt chữ cái K trước. Sau đó, để có được tất cả các biến thể có chữ cái đầu tiên K, bạn cần liệt kê tất cả sự kết hợp có thể có của các chữ cái trong các vị trí n - 1 còn lại v.v. (xem hình).
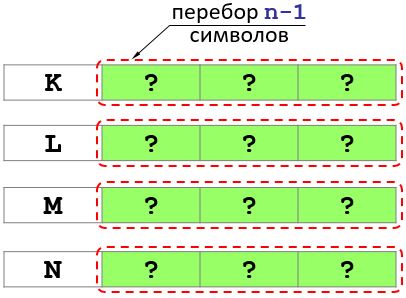 Như vậy, bài toán rút gọn thành việc giải bốn bài toán có độ dài n - 1.
Lặp lại n ký tự một cách đệ quy
w[0]='K'; // lặp qua L-1 ký tự cuối cùng
w[0]='L'; // lặp qua L-1 ký tự cuối cùng
w[0]='M'; // lặp qua L-1 ký tự cuối cùng
w[0]='N'; // lặp qua L-1 ký tự cuối cùng
w - một chuỗi ký tự lưu trữ từ đang hoạt động.
Do đó, chúng ta có đệ quy. Chúng ta có thể sắp xếp lời giải của bài toán dưới dạng một thủ tục đệ quy.
Nó vẫn còn để xác định khi nào đệ quy sẽ kết thúc? Khi tất cả các ký tự được đặt, nghĩa là số lượng ký tự được đặt là n. Trong trường hợp này, bạn cần hiển thị từ kết quả trên màn hình và thoát khỏi quy trình.
Chương trình C++ sẽ trông như thế này.
#include<iostream>
sử dụng không gian tên std;
void TumbaWords( string A, string &w, int N )
// w - tham số có thể thay đổi (kết quả chuỗi)
// Thủ tục TumbaWords được truyền bảng chữ cái dưới dạng chuỗi ký tự,
// từ word và số lượng ký tự đã được thiết lập (trước – 0).
{
int tôi;
nếu (N == w.size())
{
// nếu tất cả các ký tự đã được đặt thành từ,
// thì cần xuất ra 1 chuỗi và kết thúc thủ tục
cout << w<< kết thúc;
trở lại;
}
cho ( i = 1; i < A.size(); i ++ )
{
// nếu điều kiện trên là sai (nghĩa là không phải tất cả các ký tự đều cách nhau,
// sau đó trong vòng lặp, chúng ta duyệt qua tất cả các ký tự trong bảng chữ cái và
// luân phiên đặt ký tự vào không gian trống đầu tiên
w[N] = A[i];
Từ Tumba ( A, w, N+1 );
}
}
chủ yếu()
{
intn;
từ chuỗi;
intn;
cin>> N;
từ.resize(n); // tăng chuỗi lên kích thước n
TumbaWords("KLMN", từ, 0 );
}
LƯU Ý rằng w là một tham số có thể thay đổi (chuỗi kết quả)!
|
|