Sắp xếp chèn
Sắp xếp chèn (Sắp xếp chèn) — ;thuật toán sắp xếp trong đó các phần tử của chuỗi đầu vào được tra cứu cùng một lúc và mỗi phần tử mới đến được đặt ở vị trí thích hợp trong số các phần tử đã sắp xếp trước đó.
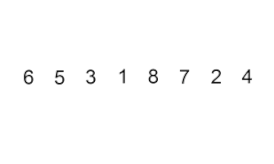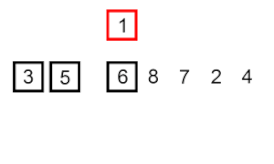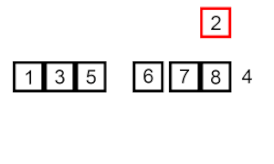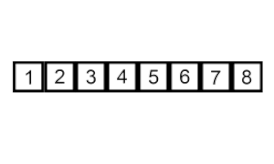
Sắp xếp chèn – nó là một thuật toán rất đơn giản nhưng không hiệu quả, tuy nhiên có một số lợi thế cụ thể khiến nó trở nên phù hợp ngay cả sau khi nhiều thuật toán khác nói chung hiệu quả hơn đã được phát triển.
Với sắp xếp chèn, bạn không cần phải sắp xếp toàn bộ mảng trước khi sắp xếp. Thuật toán có thể nhận từng phần tử một trong quá trình sắp xếp. Điều này rất hữu ích nếu chúng ta cần thêm nhiều phần tử hơn trong quá trình sắp xếp. Thuật toán sẽ chèn phần tử mới vào đúng vị trí mà không cần "thực hiện lại" sắp xếp toàn bộ mảng.
Sắp xếp chèn có thể được sử dụng trong thực tế do tính hiệu quả của nó trên các tập dữ liệu nhỏ (~10 phần tử).
Vấn đề là thế này: có một phần của mảng đã được sắp xếp, và bạn muốn chèn các phần tử còn lại của mảng vào phần đã sắp xếp mà vẫn giữ nguyên trật tự. Để làm điều này, ở mỗi bước của thuật toán, chúng ta chọn một trong các phần tử dữ liệu đầu vào và chèn nó vào vị trí mong muốn trong phần đã được sắp xếp của mảng, cho đến khi toàn bộ tập dữ liệu đầu vào được sắp xếp. Phương pháp chọn phần tử tiếp theo từ mảng đầu vào là tùy ý, nhưng thông thường (và để có được thuật toán sắp xếp ổn định), các phần tử được chèn theo thứ tự xuất hiện của chúng trong mảng đầu vào.
Thuật toán thực hiện thuật toán này
// Phần tử null được coi là một dãy đã được sắp xếp.
// Do đó, vòng lặp bắt đầu từ 1
LOOP FOR I=1 TO N-1 BƯỚC 1
X=A[I]
J=tôi
WHEN J>0 AND A[J-1]>X //đang tìm chỗ chèn
TRAO ĐỔI A[J],A[J-1]
J=J-1
KẾT THÚC
A[J]=X
TIẾP THEO TÔI
Độ phức tạp tính toán: \(\displaystyle O(n^{2})\).