|
|
Thay vì chỉ tính toán hàm băm của một chuỗi, chúng ta có thể lưu trữ giá trị tại mỗi tiền tố của nó. Lưu ý rằng đây sẽ là các giá trị băm cho các chuỗi bằng tiền tố tương ứng.
Với cấu trúc như vậy, bạn có thể nhanh chóng tính toán giá trị băm cho bất kỳ phân đoạn con nào của chuỗi này (tương tự như tổng tiền tố).
Nếu chúng ta muốn tính hàm băm của phân đoạn con [l;r], thì chúng ta cần lấy hàm băm trên tiền tố r và trừ hàm băm trên tiền tố l-1 nhân với p thành lũy thừa của r-l+1. Tại sao điều này trở nên rõ ràng nếu bạn viết các giá trị trên các tiền tố và xem điều gì sẽ xảy ra. Tôi hy vọng bạn thành công khi nhìn vào bức tranh này.
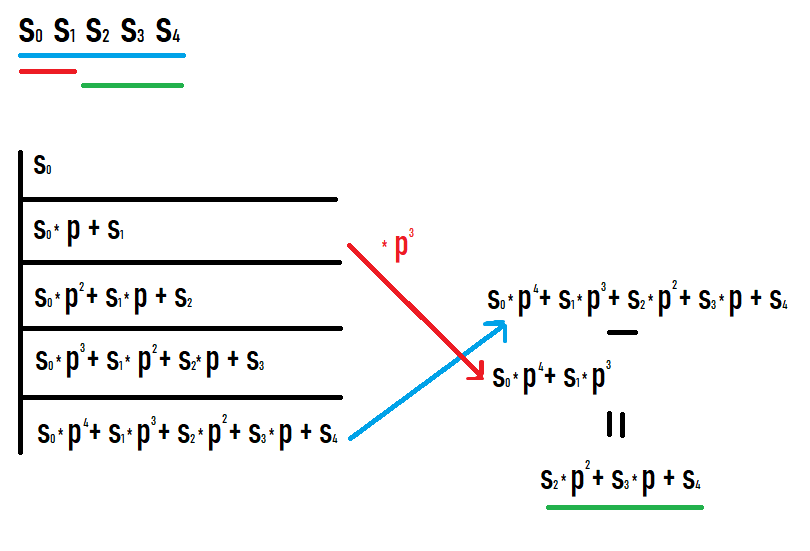
Kết quả của những hành động như vậy, chúng tôi nhận được một hàm băm của một phân đoạn con của chuỗi ban đầu. Ngoài ra, giá trị băm này bằng với giá trị đó nếu nó được coi là giá trị băm từ một chuỗi tương đương với phân đoạn con này (không cần chuyển đổi thêm độ hoặc tương tự để so sánh với các giá trị khác).
Ở đây có hai điểm cần làm rõ:
1) Để nhân nhanh lũy thừa r-l+1 với p, cần phải tính toán trước tất cả các lũy thừa có thể có của p modulo mod.
2) Cần phải nhớ rằng chúng tôi thực hiện tất cả các phép tính modulo modulo, và do đó, có thể xảy ra rằng sau khi trừ các giá trị băm tiền tố, chúng tôi sẽ nhận được một số âm. Để tránh điều này, bạn luôn có thể thêm mod trước khi trừ. Ngoài ra, đừng quên lấy giá trị modulo sau các phép nhân và tất cả các phép cộng.
Trong mã nó trông như thế này:
#include <bits/stdc++.h>
sử dụng không gian tên std;
typedef dài dài;
const int MAXN = 1000003;
// cơ sở và mô-đun băm
sẽ p, mod;
// tiền tố băm và số mũ p
h[MAXN], pows[MAXN];
// tính toán giá trị băm của phân đoạn con [l;r]
sẽ get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int chính ()
{
// bằng cách nào đó lấy p và mod
// tính trước lũy thừa p
pows[0] = 1;
for (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// giải quyết vấn đề chính
//
trả về 0;
}
|
Nếu chúng ta có hàm băm của chuỗi A bằng hA và hàm băm của chuỗi B bằng hB, thì chúng ta có thể tính nhanh hàm băm của chuỗi AB:
hAB = hA * p|B| + hB <- đếm mọi thứ theo modulo
nơi |B| - chiều dài của chuỗi B.
|
Ngoài các chuỗi, bạn cũng có thể băm các tập hợp. Đó là, tập hợp các đối tượng không có thứ tự trên chúng. Nó được tính theo công thức sau:
hash(A) = \(\sum_{a \in A} p^{ord(a)}\) <- đếm mọi thứ theo modulo
trong đó ord là một hàm gán cho một đối tượng của tập hợp số thứ tự tuyệt đối của nó trong số tất cả các đối tượng có thể (ví dụ: nếu các đối tượng là số tự nhiên thì ord(x) = x và nếu là chữ cái Latinh viết thường thì ord(& #39;a') = 1, ord('b') = 2, v.v.)
Nghĩa là, đối với mỗi đối tượng, chúng tôi liên kết một giá trị bằng cơ sở với lũy thừa của số lượng đối tượng này và tổng hợp tất cả các giá trị này để có được hàm băm của toàn bộ tập hợp. Như rõ ràng từ công thức, hàm băm dễ dàng được tính toán lại nếu một phần tử được thêm vào hoặc xóa khỏi tập hợp (chỉ cần cộng hoặc trừ giá trị được yêu cầu). Cùng logic, nếu không phải các phần tử đơn lẻ được thêm hoặc bớt, mà là các tập hợp khác (chỉ cần cộng/trừ hàm băm của chúng).
Như bạn có thể hiểu, các phần tử đơn lẻ được coi là bộ kích thước 1, mà chúng ta có thể tính toán hàm băm. Và các tập hợp lớn hơn chỉ đơn giản là sự kết hợp của các tập hợp đơn lẻ như vậy, trong đó bằng cách kết hợp các tập hợp, chúng tôi thêm giá trị băm của chúng.
Thực ra, đây vẫn là hàm băm đa thức như cũ, nhưng trước hệ số tại pm , ta đã có giá trị của phần tử dãy dưới số n - m - 1 (với n là độ dài của dãy), và bây giờ đây là số phần tử trong tập hợp có số thứ tự tuyệt đối bằng m.
Trong quá trình băm như vậy, người ta phải lấy một cơ sở đủ lớn (lớn hơn kích thước đặt tối đa) hoặc sử dụng băm kép để tránh các tình huống trong đó một tập hợp các đối tượng p có số thứ tự tuyệt đối m có cùng hàm băm với một tập hợp có một đối tượng có số thứ tự tuyệt đối số thứ tự m+1.
|
Ngoài ra còn có một số cách để băm cây có rễ một cách hiệu quả.
Một trong những phương pháp này được sắp xếp như sau:
Chúng tôi xử lý các đỉnh theo cách đệ quy, theo thứ tự duyệt theo chiều sâu. Chúng ta sẽ giả định rằng giá trị băm của một đỉnh bằng p. Đối với các đỉnh có con, đầu tiên chúng ta chạy thuật toán cho chúng, sau đó thông qua các con, chúng ta sẽ tính toán giá trị băm của cây con hiện tại. Để làm điều này, hãy coi giá trị băm của các cây con là một dãy số và tính giá trị băm từ dãy này. Đây sẽ là hàm băm của cây con hiện tại.
Nếu thứ tự của các cây con không quan trọng đối với chúng tôi, thì trước khi tính toán giá trị băm, chúng tôi sắp xếp chuỗi giá trị băm từ các cây con rồi tính giá trị băm từ chuỗi đã sắp xếp.
Bằng cách này, bạn có thể kiểm tra đẳng cấu của cây - chỉ cần đếm hàm băm mà không cần thứ tự trên các phần tử con (nghĩa là mỗi lần sắp xếp các hàm băm của phần tử con). Và nếu giá trị băm của các gốc khớp nhau thì các cây đó là đẳng cấu, ngược lại thì không.
Đối với những cây chưa có gốc, mọi thứ diễn ra theo cách tương tự, nhưng trọng tâm phải được lấy làm gốc. Hoặc xem xét một cặp băm nếu có hai trọng tâm.
|