我们可以将值存储在其每个前缀处,而不是仅仅计算序列的哈希值。请注意,这些将是等于相应前缀的序列的哈希值。
有了这样的结构,就可以快速计算出这个序列的任意子段的哈希值(类似于前缀和)。
如果我们要计算子段 [l;r] 的哈希值,那么我们需要将前缀 r 上的哈希值减去前缀 l-1 上的哈希值乘以 p 的 r-l+1 次方。如果您将值写在前缀上并看看会发生什么,那么为什么会这样就很清楚了。我希望你能成功看到这张照片。
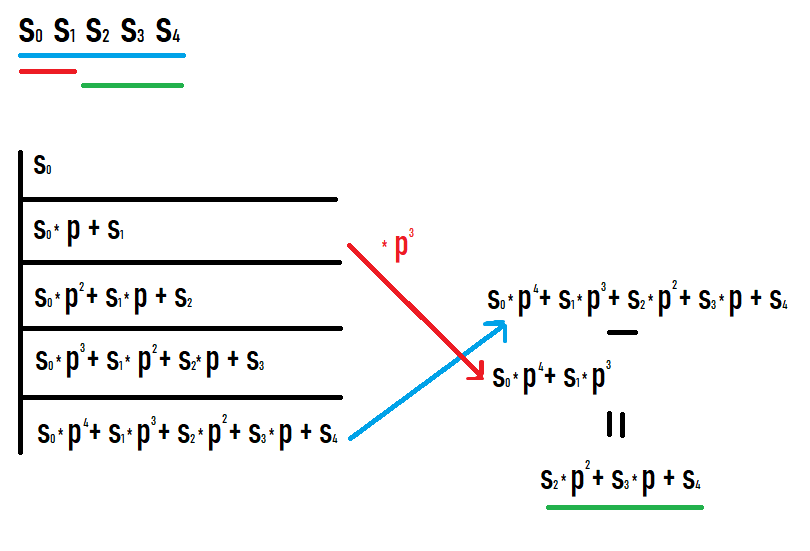
作为这些操作的结果,我们得到了原始序列的一个子段的散列。此外,如果将此散列视为来自等于此子段的序列的散列,则该散列等于该散列(不需要额外的度数转换等与其他值进行比较)。
这里有两点需要说明:
1)要快速乘以p的r-l+1次方,需要预先计算p的所有可能的次方模模。
2) 必须记住,我们执行所有计算模模,因此可能会在减去前缀哈希后得到一个负数。为避免这种情况,您始终可以在减去之前添加 mod。另外,不要忘记在乘法和所有加法之后取模值。
在代码中它看起来像这样:
#include ;
使用命名空间标准;
typedef long longll;
常数 MAXN = 1000003;
// 基础和哈希模块
ll p, mod;
// 前缀散列和指数 p
h[MAXN], pows[MAXN];
// 计算子段 [l;r] 的散列
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
主函数()
{
// 以某种方式得到 p 和 mod
// 预先计算幂 p
战俘[0] = 1;
for (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// 主要问题解决
//
返回 0;
}