Problem
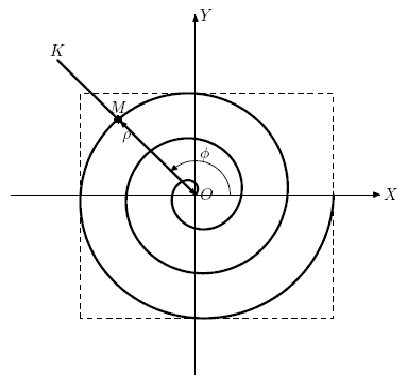
Dima 最近加入了平曲线研究所。正如这个研究所的名字所暗示的那样,它从事平面曲线领域的各种研究。最近,Dimin 的老板 Georgy 遇到了一条非常有趣的曲线,经过一番研究,它被称为阿基米德螺线。阿基米德螺线是一条平面曲线,描绘了点 M 的轨迹,它沿射线 OK 以 O 为原点匀速移动,而射线 OK 本身绕点 O 匀速旋转(见图)。换句话说,到原点的距离 rho; = OM 与旋转角度 .phi 线性相关。光束好的。在这种情况下,光线 OK 旋转相同的角度对应于相同的距离增量 ρ.
M点的移动可以通过一些参数来设置:
•初始旋转角度 .alpha。 beam OK(相对于 OX 轴的正方向逆时针测量度数);
•角速度.omega。 ray OK(以每时间单位的度数为单位);
• M点到原点(O点)的初始距离R;
• M点沿射线OK的速度V。
如果通过设置这些参数,我们不限制点M移动的时间,那么我们得到一条无限大的曲线,这是相当难以探索的。因此,Dima 决定将自己局限在研究这条曲线的某个部分,即 M 点从零时刻移动到 T 时刻所得到的那一部分。Dima 解决的问题是找到边平行于坐标轴的最小区域,可以在其中刻写。
你需要编写一个程序来找到所需的矩形
输入
输入文件包含四个整数: ω (1 ≤ omega; ≤ 100)、V (1 ≤ V ≤ 100)、R (0 ≤ R ≤ 100) 和 T (1 ≤ T ≤ 1000)。在这个问题中,假设初始旋转角度为 .alpha。为零。
输出
在输出文件的第一行打印两个实数 —所需矩形左下角的坐标,在第二行 —所需矩形右上角的坐标。
如果每个坐标的值与真实值的差异不超过 10-5,则认为答案正确。
<正文>
| 输入 |
输出 |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
奥林匹克团体赛,VKOSHP,2008 年,问题 I