Dijkstra 算法


<分区>
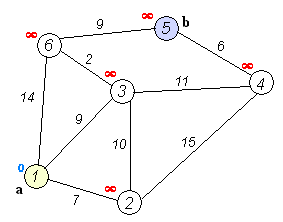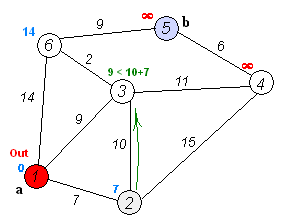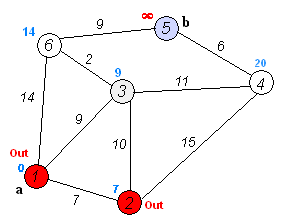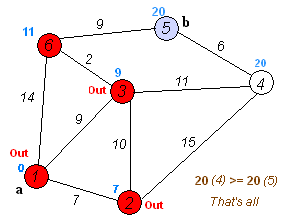
给定一个具有 n 个顶点和 m 条边的有向或无向加权图。所有边的权重都是非负的。指定了一些起始顶点。您需要找到从顶点 s 到所有其他顶点的最短路径的长度，并提供一种打印最短路径本身的方法。
 
这个问题叫做“单源最短路径问题” （单源最短路径问题）。

执行与 1-K BFS 相同的任务，但不考虑 K。此外，与 1-K BFS 一样，它不能正确处理负边缘

算法：
Dijkstra 算法本身由 N 次迭代组成。在下一次迭代中，顶点 V 从尚未标记的顶点到它的最小距离，这个顶点被标记并且相邻顶点的松弛从它发生。


 算法的最终渐近行为是：O(n2+ m)

Training problem

Dijkstra：开端 (C++)

Training problem

迪克斯特拉

由于 Dijkstra 算法的原始实现的渐近行为是： \(O(n^2 + m)\)，那么随着顶点数量的增加，工作速度变得不尽如人意。
 可以使用各种数据结构进行改进： Fibonacci 堆、集合 集合或优先队列 priority_queue。 
考虑一个带有 set 的例子，结果，最终的渐近线是： \(O(n log (m))\) , 详情。

Training problem

O(M logN) c 集合中的 Dijkstra 算法：开始 (C++)