插入排序
插入排序 (插入排序) — ;一次查找输入序列的元素的排序算法,每个新的传入元素被放置在先前排序的元素中的适当位置。
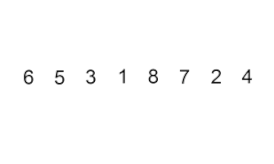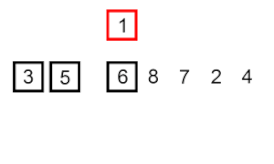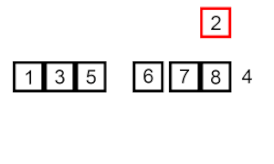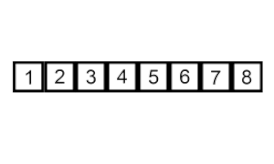
插入排序 –这是一种非常简单但效率低下的算法,但具有几个特定的优点,即使在开发了许多其他通常更有效的算法之后,它仍具有相关性。
使用插入排序,您不必在排序前就拥有整个数组。该算法可以在排序过程中一次接收一个元素。如果我们需要在排序期间添加更多元素,这非常方便。 算法会在正确的位置插入新元素而不用“重新执行”对整个数组进行排序。
由于插入排序在小型(约 10 个元素)数据集上的效率,因此可以在实践中使用。
问题是这样的:数组中有一部分已经排好了序,你想把数组剩下的元素插入排好序的部分,同时保持顺序。为此,在算法的每个步骤中,我们选择一个输入数据元素并将其插入数组中已排序部分的所需位置,直到对整个输入数据集进行排序。从输入数组中选择下一个元素的方法是任意的,但通常(并且为了获得稳定的排序算法),元素是按照它们在输入数组中出现的顺序插入的。
该算法的算法实现
<前>
// null 元素被认为是一个已经排序的序列。
// 因此,循环从1开始
循环 I=1 到 N-1 第 1 步
X=A[我]
J=我
WHEN J>0 AND A[J-1]>X //寻找插入的地方
交换 A[J],A[J-1]
J=J-1
结束再见
A[J]=X
下一个
计算复杂度:
\(\displaystyle O(n^{2})\)。