(Java) 子程序。递归。

过程或函数可能包含对其中另一个过程的调用。其中，子程序可以调用自身。在这种情况下，计算机不关心。他也一如既往，从上到下始终如一地执行他遇到的命令。

如果你还记得数学，那你就会遇到 数学归纳原理。具体如下：

对于每个自然 n 如果
    1. 对 n = 1 和
有效     2. 从对任意自然数 n = k 的陈述的有效性，可以得出它对  n = k+1 为真。

在编程中，这种技术称为递归

递归是一种根据给定的简单基本情况根据集合本身定义一组对象的方法。

Recursive 也将被称为过程（函数），直接或通过其他过程和函数调用自身
递归过程的一个例子： <代码>static void Rec(int a) { 如果 (a>0) Rec(a-1); 输出 << A; } 示意性地，递归的工作可以用流程图表示

 

Rec() 过程以参数 3 执行。然后，在参数 3 的过程中，调用参数 2 的过程，依此类推，直到调用参数 0 的过程。当过程带有参数 0 被调用，递归调用已经不会发生，参数 0 的过程将打印数字 0 并终止。然后控制权返回给参数为 1 的过程，它也通过打印数字 1 来完成它的工作，依此类推。在带有参数 3 的过程之前。 

所有被调用的过程都存储在内存中，直到它们完成它们的工作。并发过程的数量称为递归深度。

我们已经看到，递归是重复执行子程序中包含的指令。反过来，这类似于循环的工作。有些编程语言根本不存在循环结构，例如 Prolog。 
我们来模拟一下for循环的运行。 
for 循环包含一个计步器变量。在递归子程序中，这样的变量可以作为参数传递。 //LoopImitation() 过程有两个参数 //第一个参数–计步器，第二个参数——总步数 void LoopImitation(int i, int n) { 输出 << “你好” <<我 <<结束； // 对 i 的任何值重复的运算符 if (i < n) //直到循环计数器等于值n， { //使用 i+1 参数调用过程的新实例（转到下一个 i 值） LoopImitation(i+1, n); }

迭代 在编程中—从广义上来说——数据处理的组织，其中的动作重复多次，而不会导致对自身的调用（不像  %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursion" >递归)。狭义上——一步循环数据处理过程。 
当前步骤（迭代）的迭代算法通常使用在先前步骤计算的相同操作或动作的结果。  此类计算的一个例子是递归关系的计算。 
递归值的一个简单示例是阶乘：\(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\) 每一步（迭代）的值的计算是 \(N=N \cdot i\) 。 在计算\(N\)的值时，我们取已经存储的值 \(N\) >.

一个数的阶乘也可以用递归公式来描述：



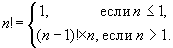
你可能会注意到这个描述只不过是一个递归函数。
这里是第一行 (\(n <= 1\)) —这是基本情况（递归的结束条件），第二行是到下一步的过渡。 
  <正文>
应该理解，函数调用涉及一些额外的开销，因此非递归阶乘计算会稍微快一些。 
结论： 如果您可以使用简单的迭代算法编写程序，无需递归，那么您就需要编写无递归的程序。但是，仍然存在一大类仅通过递归实现计算过程的问题。
另一方面，递归算法通常更容易理解。
 

递归阶乘函数看起来像这样	以通常的非递归方式比较求阶乘的算法
int 阶乘（int n）{ 如果 (n > 1) 返回 n * 阶乘（n - 1）； 否则返回 1；	x = 1; 对于 (i = 2; i <= n; i++) x = x * 我; printf("%d",x);
您可能会发现此信息很有用： 英文字母'\(A\)'代码为 65 进入 \(char \ c = 65;\) 在变量\(c\) \(A\)  因此，您可以通过其代码获得所需的字母 Training problem 数字转十六进制数系统