| Problem description | | Progress |
|
Темы:
USE
Using sort
The store purchases bolts (bolt) and nuts (nut), for which a certain amount of money is allocated. The hardware plant has various modifications of these products at a retail price. When buying, the manager is guided by the following rules:
- You need to buy as many items as possible, regardless of their type and modification.
- If you can buy the maximum number of products in different ways, you need to choose the method that will buy the most nuts.
- If you can buy the maximum number of products with the same number of nuts in different ways, you need to choose the method in which the entire purchase will be cheaper.
Determine how many nuts will be bought in total and how much will remain unused.
Input
The program receives several lines as input. The first line contains two numbers separated by a space: N - the total number of bolts and nuts at the hardware plant and M - the amount of money allocated for the purchase (in rubles). Each of the next N lines contains an integer (price of the product in rubles) and the type of product (bolt - bolt, nut - nut). All data in the lines is separated by a single space.
Imprint
In your answer, write down two whole numbers: first, the number of nuts purchased, then the remaining unused amount of money.
Examples
| # |
Input |
Output |
| 1 |
6 6500
1500 bolt
500 bolt
3500 nut
3000 nut
2500 bolt
1000 nut
2 500 |
|
| |
![]()
|
|
Темы:
USE
Using sort
The store purchases bolts (bolt) and nuts (nut), for which a certain amount of money is allocated. The hardware plant has various modifications of these products at a retail price. When buying, the manager is guided by the following rules:
- You need to buy as many items as possible, regardless of their type and modification.
- If you can buy the maximum number of items in different ways, you need to choose the method that will buy the most bolts.
- If you can buy the maximum number of products with the same number of bolts in different ways, you need to choose the method in which the entire purchase will be cheaper.
Determine how many bolts will be purchased in total and how much will remain unused.
Input
The program receives several lines as input. The first line contains two numbers separated by a space: N - the total number of bolts and nuts at the hardware plant and M - the amount of money allocated for the purchase (in rubles). Each of the next N lines contains an integer (price of the product in rubles) and the type of product (bolt - bolt, nut - nut). All data in the lines is separated by a single space.
Imprint
In your answer, write down two whole numbers: first, the number of bolts purchased, then the remaining unused amount of money. (in one line with one space)
Examples
| # |
Input |
Output |
| 1 |
6 6500
1500 nuts
500 nut
3500 bolt
3000 bolt
2500 nut
1000 bolt
2 500 |
|
| |
![]()
|
|
Темы:
USE
Using sort
The store purchases bolts (bolt), nuts (nut), nails (pin), washers (shim) and screws (screw), for which a certain amount of money has been allocated. The hardware plant has various modifications of these products at a retail price. When buying, the manager is guided by the following rules:
- You need to buy as many items as possible, regardless of their type and modification.
- If you can buy the maximum number of two different products in different ways, you need to choose the method that will buy the most nuts.
- If you can buy the maximum number of products with the same number of nuts in different ways, you need to choose the method in which the entire purchase will be cheaper.
Determine how many nuts will be bought in total and how much will remain unused.
Input
The program receives several lines as input. The first line contains two numbers separated by a space: N - the total number of bolts and nuts at the hardware plant and M - the amount of money allocated for the purchase (in rubles). Each of the next N lines contains an integer (price of the product in rubles) and the type of the product. All data in the lines is separated by a single space.
Imprint
In your answer, write down two whole numbers: first, the number of bolts purchased, then the remaining unused amount of money. (in one line with one space)
Examples
| # |
Input |
Output |
| 1 |
6 1650
600 screw
750 bolt
750 nut
450 pin
300 nut
150 bolt
2 0 |
|
| |
![]()
|
|
Темы:
USE
Using sort
The store purchases bolts (bolt), nuts (nut), nails (pin), washers (shim) and screws (screw), for which a certain amount of money has been allocated. The hardware plant has various modifications of these products at a retail price. When buying, the manager is guided by the following rules:
- You need to buy as many items as possible, regardless of their type and modification.
- If you can buy the maximum number of two different items in different ways, you need to choose the method that will buy the most bolts.
- If it is possible to buy the maximum number of products in different ways with the same number of other products, you need to choose the method in which the entire purchase will be cheaper.
Determine how many bolts will be purchased in total and how much will remain unused.
Input
The program receives several lines as input. The first line contains two numbers separated by a space: N - the total number of bolts, nuts, nails, washers and screws from the hardware plant and M - the amount of money allocated for the purchase (in rubles). Each of the next N lines contains an integer (price of the product in rubles) and the type of the product. All data in the lines is separated by a single space.
Imprint
In your answer, write down two whole numbers: first, the number of bolts purchased, then the remaining unused amount of money. (in one line with one space)
Examples
| # |
Input |
Output |
| 1 |
6 1650
600 screw
750 bolt
750 shim
450 pin
300 nut
150 bolt
2 0 |
|
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \((\bar y \wedge (x \equiv \bar w)) \wedge (z \vee x)\). At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
| ? |
? |
? |
? |
F |
| 0 |
1 |
|
0 |
1 |
| 1 |
1 |
|
|
1 |
| |
|
|
1 |
1 |
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
For a natural number N , determine the parity of the maximum divisor not equal to N and 1. Print the maximum divisor itself and the word "even", separated by a space, if the maximum divisor is even, and the word "odd" - if odd.
Input
The input is not a simple natural number N (1 <= N <= 109).
Imprint
Print the answer on the screen first, the maximum divisor of the number, then, separated by a space, the word "even", if the maximum divisor is even, and the word "odd" - if odd.
Examples
| |
![]()
|
|
Темы:
USE
Given a natural number N - the number of numbers (1<=N<=103), and natural numbers ai (1<=ai<=105 ). For each number ai determine the smallest natural number m less than ai that has the maximum number of different divisors.
Input
In the first line, the program receives a natural number N (1<=N<=103) as input. The following N lines set the numbers ai (1<=ai<=10 5), each number on a separate line.
Imprint
For each number ai print the number m - the smallest natural number less than ai, which has the maximum number of different divisors. Each number m must be printed on a separate line.
Examples
| # |
Input |
Output |
| 1 |
5
440
552
953
53
175 |
360
360
840
48
120
|
| |
![]()
|
|
Темы:
USE
Given a natural number N - the number of numbers (1<=N<=103), and non-prime natural numbers ai< /sub> (1<=ai<=105). For each number ai print its smallest and largest divisors not equal to 1, 2, 3 and ai< /sub>/2, ai/3, ai.
Input
In the first line, the program receives a natural number N (1<=N<=103) as input. The following N lines give numbers ai (100<=ai<=10 5), each number on a separate line.
Imprint
For each number ai print two space-separated numbers on a separate line - its smallest and largest divisors other than 1, 2, 3 and ai/2, ai/3, a i.
Examples
| # |
Input |
Output |
| 1 |
5
731
1034
460
618
667 |
17 43
11 94
4 115
6 103
23 29 |
| |
![]()
|
|
Темы:
USE
Write a program that searches among the integers belonging to the numerical interval [1014260; 3025423], prime numbers. Print the first 20 found prime numbers in ascending order, to the left of each number print its number in order.
Example of displaying the first 3 numbers
1 1014263
2 1014287
3 1014301
...
You need to output all numbers from the given range.
| |
![]()
|
|
Темы:
USE
Let M – the sum of the minimum and maximum natural divisors of an integer, not counting one and the number itself. If the number does not have such divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 700 000, in ascending order and looks for those for which M ends in 8 code>. Print the first five found numbers
and their corresponding M.
values
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the difference (modulo) of two paired natural divisors of an integer not equal to one and the number itself. If the number does not have such divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 1 000 000, in ascending order and searches among them for those that have at least one value of M such that 0 < M < 1000 . Print the first five found numbers and their corresponding M values. If the number of suitable M values has more than one, then output the M value formed by the difference with the minimum divisor not equal to 1.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – M value (one space apart). Lines are displayed in ascending order of found numbers.
Example
For the number 12, the pair divisors are the numbers:
2 and 6 (M = 4)
3 and 4 (M = 1)
In the answer, you must specify the value M = 4, since the resulting difference is formed with a minimum divisor of 2.
| |
![]()
|
|
Темы:
USE
Let M – the sum of the prime natural divisors of an integer, not counting one and the number itself. If the number does not have such divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 500 000, in ascending order and searches among them for those for which the value 10000 < M < 50000 . Print the first five found numbers
and their corresponding M.
values
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the number of different even natural nontrivial divisors of an integer, and SM is the sum of these divisors.
Write a program that iterates over integers greater than 1 000 000, in ascending order and searches among them for those with M = 5. If such the number has no divisors, then the value of SM is considered equal to zero. Print the first five found numbers and their corresponding SM values.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value SM (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of the minimum even and maximum odd natural divisors of an integer, not counting one and the number itself. If the number does not have any divisor (either even or odd), then the value of this divisor is considered equal to zero.
Write a program that iterates over integers greater than 12,000,000, in ascending order, looking for those for which 0 < M < 1,000,000 . Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of simple natural divisors of an integer, not counting one and the number itself, and KM is the number of such divisors. If the number does not have such divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 2 560 000, in ascending order and searches among them for those for which M is odd and КM= 6. Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \(w \wedge (x \vee z)\wedge(x\rightarrow y)\wedge(y\vee z)\). At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = n * n if n <= 1;
F(n) = F(n-2) + F(n/3) if n > 1 and n is a multiple of 3 but not a multiple of 2;
F(n) = F(n/2) + F(n-3) if n > 1 and n is a multiple of 2 but not a multiple of 3;
F(n) = F(n/2) + F(n/3) if n > 1 and n is a multiple of 2 and a multiple of 3;
F(n) = F(n-1) if n > 1 and n is neither a multiple of 2 nor a multiple of 3.
Find the minimum n value such that F(n) = 104.
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -10 000 to 10 000 inclusive. Determine the number of pairs of the sequence in which both numbers are even, and the sum of the elements of the pair is not more than the maximum even element of the sequence. In your answer, write down the number of found pairs, then the maximum of the sums of the elements of such pairs (two numbers separated by a space in one line). In this problem, a pair means two successive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
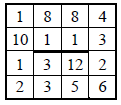
The square is lined with N × N cells (1 < N < 30). The EM executor can move around the cells by performing one of two commands in one move: right or up. On command to the right EMU moves to the adjacent right cell, on command up – to the adjacent upper one. The square is bounded by external walls. There can also be internal walls between adjacent square cells. EMU cannot pass through walls.
At the initial moment of time, the EMU has a supply of fruits equal to the number written in the starting cell. When moving from cell to cell, EMU eats a certain number of fruits. When moving to the right, the EMU eats the number of fruits recorded in the cell it moves to, plus 2 more. When moving up, the EMU eats twice the number of fruits recorded in the cell it moves to, Determine the maximum and minimum number of fruits that remain in the reserve at the EMU, passing from the lower left cell (starting cell) to the upper right one.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 | |
![]()
|
|
Темы:
USE
Sorting algorithms
The file contains positive integers. The first line of the file contains the number N - the number of numbers. The following N lines contain the numbers themselves. In your answer, write in the column the 10 largest three-digit numbers.
Assignment file
| |
![]()
|
|
Темы:
USE
Using sort
The file contains positive integers. The first line of the file contains the number N - the number of numbers, and the natural number S. The following N lines contain the actual numbers.
In your answer, indicate two numbers separated by a space: first, the maximum number of numbers that must be added so that the sum does not exceed the number S, then the value of the resulting sum.
| |
![]()
|
|
Темы:
Using sort
USE
In the set of numbers N, replace one number with a number from the set of numbers M so that the sum of the numbers in the set N is as close as possible to the number < code>S. Print three numbers, each on a separate line:
1 line - the number that was replaced from the set N;
2nd line - the number from the set M, which was replaced;
Line 3 - the resulting sum of numbers from the set N.
It is guaranteed that such a substitution can be made. If possible substitutions several, then choose the one in which the number from the N set is less.
Input
In the first line, enter 3 numbers separated by a space: n (10<=N<=105) - the number of numbers in the set N, < code>m (10<=M<=105) - number of numbers in set M, S ( 10<=S<=109) S>sum(N), where sum(N) is the sum of all numbers in the set < code>N.
The second line contains a set of numbers N: n numbers separated by one space (each number modulo does not exceed 105).
The third line contains a set of numbers M: m numbers separated by one space (each number modulo does not exceed 105).
Imprint
Display the answer to the problem as specified in the condition.
Examples
| # |
Input |
Output |
| 1 |
2 2 10
24
1 3
| 2
3
7 |
| |
![]()
|
|
Темы:
USE
Using sort
The system administrator creates an archive of user files once a week. However, the size of the disk where it places the archive may be less than the total size of the archived files. It is known how much space each user's file occupies. Given information about the size of user files and the free space on the archive disk, determine the maximum number of users whose files can be archived, as well as the maximum size of an existing file that can be stored in the archive, provided that the files of the maximum possible number of users are saved. Write a program that calculates the maximum number of users whose files can be archived, as well as the maximum size of an existing file that can be archived, provided that the files of the maximum possible number of users are stored.
Input:
The first line contains two numbers: S – free disk space (a natural number not exceeding 100,000) and N – number of users (a natural number not exceeding 10000). The next N lines contain the values of each user's file sizes (all natural numbers, not exceeding 100), each on a separate line.
Output:
Print two space-separated numbers on one line: first, the largest number of users whose files can be archived, then the maximum size of an existing file that can be archived, provided that the files of the maximum possible number of users are stored.
Example
| # |
Input |
Output |
| 1 |
100 4
80
30
50
40 |
2 50 |
With this initial data, you can save the files of a maximum of two users. The possible sizes of these two files are 30 and 40, 30 and 50 or 40 and 50. The largest file size of the listed – 50, so the answer for this example is: 2 50
| |
![]()
|
|
Темы:
Using sort
USE
In quizzz "Pass the exam for 100 points" You can score up to 10,000 points. At the end of the game, the first K participants who scored the most points receive a bonus to their points in the form of +30% of the scores. You know the information about how many points each participant in the game scored. Determine the maximum number of points that the bonus did not apply to, as well as the integer part of the total bonus amount received by the players.
Input and output data
The first line input file contains two numbers separated by spaces: N – total number of players (a natural number not exceeding 10,000) and K – the number of players who receive the bonus. The following N lines contain the results of each participant (the number of points scored - all natural numbers not exceeding 10,000), each in a separate line.
Write down two numbers in your answer: first, the maximum number of points to which the bonus did not apply, and then the whole part of the sum of all bonuses.
Example input file:
12 4
370
580
3000
1310
1700
2810
1660
1250
1870
1340
1400
1260
With such initial data, the answer should contain two numbers – 1660 2814.
| |
![]()
|
|
Темы:
Using sort
USE
Ded Moroz's factory produces light bulbs of various weights and brightness. The weight of the bulb does not exceed 100 grams, the brightness of the bulb does not exceed 10,000 lumens.
K of the brightest light bulbs are selected to make a New Year's garland. If the brightness of two bulbs is the same and they all do not fit in a garland, then place a bulb with a smaller weight.
Information is known about the weight and brightness of each light bulb brought to the workshop to form a New Year's garland.
Determine the total weight of the bulbs in the garland and the average brightness of the entire garland.
Input and output data
In file in the first line space-separated numbers N are written - the number of light bulbs brought to the workshop (natural number, not exceeding 1000) and K – the number of light bulbs in the garland (a natural number not exceeding 100). Each of the following N lines contains two numbers – the weight and brightness of each bulb.
Write in the answer two numbers – first, the total weight of the bulbs in the garland, then the average brightness of the entire garland (only the whole part).
An example of the organization of source data in the input file:
9 4
50 600
60 480
45 540
30 300
15 180
70 560
30 360
91 910
40 320
Response: 256 652
| |
![]()
|
|
Темы:
Count sort
USE
For the performance, the gymnasts use ribbons, which are placed on the table after the performance. The father of the best gymnast Anna K., in anticipation of the award, decided to write down the coordinates of the beginning and end of the ribbons. Do you have a file with this information. Determine at how many points of the table the greatest thickness of the coating turned out and what it is equal to. The table has a length Lmm. At the end of the performance of all the gymnasts, there was N ribbons. No ribbon protrudes beyond the table. All ribbons lie horizontally. The ribbons stack on top of each other.
Input
The first line of the file contains two numbers - L, N (1 <= L <= 10000, 1 <= N <= 10000). The following N lines contain 2 numbers each - l, r (1 <= l <= r < = L) - left and right ends of ribbons relative to the left edge of the table.
In your answer, indicate two numbers separated by a space - the maximum thickness of the tape table cover and the number of points with such a thickness.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 0 if n <= 0;
F(n) = F(n - 2) if n > 0, the last digit of the number n is even and the number n is not a multiple of 4;
F(n) = F(n / 4) + F(n - 2) if n > 0, number n is a multiple of 4;
F(n) = n + F(n - 1) if n > 0 and n odd;
How many different values of n, less than 100 will result in F(n) ending in 1?
| |
![]()
|
|
Темы:
USE
Logic and sets
Two segments are given on the number line: B = [10; 20] and C = [12; 30]. Specify the smallest possible length of such a segment A for which the logical expression
\((x \notin B) \rightarrow ((x \in C) \rightarrow (x \in B)) \ vee \neg((x \notin A) \wedge (x \in C))\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
Two segments are given on the number line: B = [10; 35] and C = [25; 49]. Specify the largest possible length of such segment A for which the logical expression
\((x \in A) \rightarrow \neg((x \in B) \equiv (x \in C) )\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
Two segments are given on the number line: B = [10; 40] and C = [15; 50]. Specify the smallest possible length of such a segment A for which the logical expression
\(((x \notin A) \wedge (x \in B)) \rightarrow ((x \in C) \rightarrow (x \in A))\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
Three segments are given on the number line: B = [5; 30], C = [1; 20] and D = [25; 45]. Specify the largest possible length of such segment A for which the logical expression
\((x \in A) \rightarrow (((x \notin B) \vee (x \notin C)) \rightarrow (x \in D))\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, passing through city G?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, passing through city B?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, passing through city B?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, passing through city G?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L passing through city D?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, passing through city G?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L passing through city D?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L passing through city K?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, but not passing through city B?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, but not passing through city D?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, but not passing through city Z?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, D, E, W, H, I, K, L, M. On each road, you can move only in one direction, indicated by the arrow. How many different ways are there from city A to city M that do not pass through city D?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, E, F, W, H, I, K, L. You can move along each road only in one direction, indicated by the arrow. How many exist different paths from city A to city L, but not passing through city E?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, D, E, W, H, I, K, L, M. On each road, you can move only in one direction, indicated by the arrow. How many different ways are there from city A to city M that do not pass through city I?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads connecting the cities A, B, C, D, D, E, W, H, I, K, L, M. On each road, you can move only in one direction, indicated by the arrow. How many different paths are there from city A to city M passing through city I?
(Image can be enlarged by clicking on it. Will open in a new window)
| |
![]()
|
|
Темы:
Number systems
USE
The value of an arithmetic expression
\(3 \cdot 4^{47} + 4 ^{32}- 4^{25} -2 \cdot 4 ^{20}-8\)
written in the number system with base 16. How many digits 'F' contained in this post?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3 \cdot 4^{47} + 2 \cdot 4 ^{39}+3 \cdot 4^{37 } + 2 \cdot 4^{36}+3 \cdot 4^{32}+1\)
written in the number system with base 8. How many significant zeros are in this entry?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3 \cdot 4^{39} + 2 \cdot 4 ^{36}- 2 \cdot 4^{32 } - 4^5-2 \cdot 4^2+1\)
written in the number system with base 16. How many digits 'F' contained in this post?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(2 \cdot 4^{47} + 2 \cdot 4 ^{44}- 2 \cdot 4^{39 } - 2 \cdot 4^{37}-3 \cdot 4^{36}+1\)
written in the number system with base 4. How many significant zeros are in this entry?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(2 \cdot 4^{84} + 3\cdot4 ^{42}- 2\cdot4^{34}+ 2 \cdot 4^{17}+3\cdot 4^{3} +16\)
written in the number system with base 4. How many 3 digits does this entry contain?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3 \cdot 4^{84} + 4 ^{83}- 4^{63} - 3 \cdot 4 ^{42}+4^{40} - 4^{38}+3\)
written in the number system with base 8. How many 7 digits does this entry contain?
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -10 000 to 10 000 inclusive. Determine the number of pairs in the sequence in which the sum of the numbers is a multiple of three and both numbers are less than the arithmetic mean of all even numbers in the sequence. In your answer, write down the number of found pairs, then the minimum of the sums of the elements of such pairs (two numbers separated by a space in one line). In this problem, a pair means two successive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -10 000 to 10 000 inclusive. Determine the number of pairs in the sequence in which at least one element is a divisor of the sum of all numbers in the sequence. In your answer, write down the number of found pairs, then the minimum of the sums of the elements of such pairs (two numbers separated by a space in one line). In this problem, a pair means two successive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -10 000 to 10 000 inclusive. Determine the number of pairs of the sequence in which both numbers are even, and the sum of the elements of the pair is not more than the minimum odd element of the sequence. In your answer, write down the number of found pairs, then the maximum of the sums of the elements of such pairs (two numbers separated by a space in one line). In this problem, a pair means two successive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -10 000 to 10 000 inclusive. Determine the number of pairs of the sequence in which both numbers end in F in the hexadecimal number system, and the sum of the elements of the pair has the same sign as the sum of all elements divisible by 16. In your answer, write down the number of found pairs, then the maximum from the sums of the elements of such pairs (two numbers separated by a space in one line). In this problem, a pair means two successive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -10 000 to 10 000 inclusive. Determine the number of triples in the sequence in which the sum of the last digits of each of the numbers is an even number, and the minimum of these numbers is not less than the minimum odd among all the numbers in the sequence. In your answer, write down the number of triples found, then the maximum number of all such triples (two numbers separated by a space on one line). In this task, under a triple means three consecutive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -15000 to 15000 inclusive. Determine the number of triples in the sequence in which all three numbers form an increasing sequence, and the sum of the numbers in the triple has the same parity as the sum of all the numbers. In your answer, write down the number of triples found, then the maximum of the sums of the elements of such triples (two numbers separated by a space in one line) . In this task, under a triple means three consecutive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -15000 to 15000 inclusive. Determine the number of triples in the sequence in which the second element is less than both of its neighbors, and at the same time the sum of the numbers in the triple has the opposite sign from the sum of all numbers. In your answer, write down the number of triples found, then the minimum of the sums of the elements of such triples (two numbers separated by a space in one line) . In this task, under a triple means three consecutive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -15000 to 15000 inclusive. Determine the number of triples in the sequence in which the third number is not less than the sum of the first two, and the sum of the first two is not greater than the sum of all numbers in the file that are multiples of 15. In your answer, write down the number of triples found, then the maximum sum of all the sums of the first two numbers (two numbers separated by a space in one line). In this task, under a triple means three consecutive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
The file contains a sequence of integers. Sequence elements can take integer values from -15000 to 15000 inclusive. Determine the number of triples in the sequence in which the second element is greater than both of its neighbors, and the sum of the numbers in the triple has the same sign as the sum of all the numbers. In your answer, write down the number of triples found, then the maximum of the sums of the elements of such triples (two numbers separated by a space in one line) . In this task, under a triple means three consecutive elements of a sequence.
Assignment file
| |
![]()
|
|
Темы:
USE
Logic and sets
Two segments are given on the number line: B = [5; 15], C = [30; 60]. Specify the smallest possible length of such a segment A for which the logical expression
\((x \notin A) \rightarrow \neg((x \in B) \wedge (x \notin C) \vee (x \in C))\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
Two segments are given on the number line: B = [40; 80], C = [120; 150]. Specify the largest possible length of such segment A for which the logical expression
\((((x \notin C)\rightarrow (x \in B)) \rightarrow (x \in B) ) \rightarrow ((x \notin A) \vee (x \in B))\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
Three segments are given on the number line: B = [0; 50], C = [25; 60] and D = [35; 80]. Specify the largest possible length of such segment A for which the logical expression
\((x \in A) \rightarrow ((x \in B) \vee (x \in D)) \ wedge (x \notin C)\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
Three segments are given on the number line: B = [0; 70], C = [30; 60] and D = [20; 90]. Specify the smallest possible length of such a segment A for which the logical expression
\((((x \in B) \rightarrow (x \in C)) \wedge (x \in D) ) \rightarrow (x \in A)\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
Three segments are given on the number line: B = [10; 40], C = [20; 85] and D = [70; 90]. Specify the largest possible length of such segment A for which the logical expression
\((x \in A) \rightarrow ((x \notin B) \rightarrow ((x \in C) \ wedge (x \in D)))\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
There are three segments on the number line: B = [25; 80], C = [60; 75] and D = [35; 70]. Specify the smallest possible length of such a segment A for which the logical expression
\(((x \in C) \neq (x \in B)) \rightarrow (x \in D) \ vee (x \in A)\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Logic and sets
There are three segments on the number line: B = [25; 80], C = [60; 75] and D = [70; 90]. Specify the smallest possible length of such a segment A for which the logical expression
\(((x \in C) \neq (x \in B)) \rightarrow (x \in D) \ vee (x \in A)\)
true (i.e. takes the value 1) for any value of the variable x.
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(2 \cdot 8^{99} + 2\cdot8 ^{30}- 2\cdot8^{85} - 2 \cdot 8^{15}+3\cdot 8^{5} -8^3- 2 \)
written in the number system with base 8. How many 7 digits does this entry contain?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(2^{234} + 2 ^{100}- 2^{43}- 2^{35}+2 ^{8} -129\)
written in the number system with base 16. How many 0 digits does this entry contain?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3 \cdot 8^{112} - 2\cdot8 ^{78}+4\cdot8^{63}- 2 \cdot 8^{35}-8^{8} -52\)
written in the number system with base 8. How many 7 digits does this entry contain?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3 \cdot 7^{112} - 2\cdot7 ^{78}+4\cdot7^{63}- 2 \cdot 7^{35}-7^{8} -52\)
written in the number system with base 7. How many significant digits of 0 does this entry contain?
| |
![]()
|
|
Темы:
USE
Word processing
The first line of the text file indicates the number of lines in the file containing various characters of the English alphabet (from A to Z). Determine the number of lines in which the number of characters denoting a vowel of the English alphabet is greater than the number of characters denoting a consonant. Please answer with one number.
To complete this task, you must write a program.
File
task24-2.txt
| |
![]()
|
|
Темы:
USE
Word processing
The text file consists of the characters M, A, R, S. Define the maximum number of consecutive characters in the attached file, among which there are no consecutive characters M. To complete this task, you must write a program.
Assignment file
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 3 if n <= 0;
F(n) = F(n / 6) + 12 if n > 0 and the number n is a multiple of 6;
F(n) = F(n - n mod 6) if n > 0 and the number n is not a multiple of 6;
What is the maximum value of n, result F(n) at most 25?
The operation a mod b calculates the remainder of dividing a by b.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 5 if n <= 0;
F(n) = F(n / 15) + F(n - 10) if n > 0, and the number n is a multiple of 15;
F(n) = F(n - 3) if n > 0, the number n when divided by 15 is 3;
F(n) = F(n - 1) + n if n > 0 and n is not a multiple of 15, and when divided by 15 the remainder is not 3;
What is the minimum value of n, for F(n) to exceed 200?
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 5 if n <= 0;
F(n) = F(n / 4) + 7 if 0 < n <= 100, and n is a multiple of 4;
F(n) = F(n - 1) + 17 if 0 < n <= 100, and n is not a multiple of 4;
F(n) = F(n - 4) if n > 100.
What is the minimum value of n, for F(n) to exceed 100?
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 0 if n <= 0;
F(n) = F(n / 3) + n if 0 < n <= 100, and the number n is a multiple of 3;
F(n) = F(n - 1) + n if 0 < n <= 100 and n is not a multiple of 3;
F(n) = F(n - 3) if n > 100.
With how many different values n, in the range [100, 250], the result F(n) will be equal to 266?
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 0 if n <= 10;
F(n) = F(n / 7) + n if 10 < n <= 200, and the number n is a multiple of 7;
F(n) = F(n - 1) + n if 10 < n <= 200 and n is not a multiple of 7;
F(n) = F(n - 7) if n > 200.
With how many different values n, in the range [1, 100], the result F(n) will be equal to n?
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 3 if n <= 0;
F(n) = F(n / 5) + n if 0 < n <= 100, and the number n is a multiple of 5;
F(n) = F(n - 1) + n if 0 < n <= 100 and n is not a multiple of 5;
F(n) = F(n - 5) if n > 100.
With how many different values n, in the range [100, 250], the value F(n) and number n will be the same parity (then are either both odd or both even)?
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 3 if n <= 10;
F(n) = F(n / 5) + n if 10 < n <= 200, and the number n is a multiple of 5;
F(n) = F(n - 1) + n if 10 < n <= 200 and n is not a multiple of 5;
F(n) = F(n - 5) if n > 200.
For how many different values n, not exceeding 250, the result F(n) will be equal to 243?
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 3 if n <= 10;
F(n) = F(n / 7) + n - 1 if 10 < n <= 200, and the number n is a multiple of 7;
F(n) = F(n - 1) + n + 1 if 10 < n <= 200 and n is not a multiple of 7;
F(n) = F(n - 7) + 7 if n > 200.
What is the smallest value of n result F(n) will be equal to 106?
| |
![]()
|
|
Темы:
USE
The text file consists of no more than 106 characters and contains only uppercase Latin letters (ABC…Z). The text is divided into lines of various lengths. It is necessary to find the string in which the sequence of letters AA occurs most often. If there are several such lines, you need to take the one that was encountered earlier in the file. Determine in this string the length of the longest subsequence in which there are no two adjacent identical letters. Write down the length of this subsequence in your answer.
Example
Source file:
AAAABABC
ZZAAAACZ
QRAAUT
In this example, the sequence AA occurs 3 times in the first and second lines, in the third – 1. We take the first line, because it is in the file before. This line contains the longest subsequence that does not contain two adjacent identical letters ABABC, its length is 5. In the answer for this example, write 5.
Assignment file
| |
![]()
|
|
Темы:
USE
The text file consists of no more than 106 characters and contains only uppercase Latin letters (ABC…Z). The text is divided into lines of various lengths. It is necessary to find a string that contains the longest subsequence between two letters A (the first and last letters of A are also included in the subsequence) and other letters A is not in this subsequence. If there are several such lines, you need to take the one that was encountered earlier in the file. Determine which letter occurs most often in this subsequence. If there are several such letters, you need to take the one that is earlier in the alphabet. Write down the found letter in the answer, as well as how many times it occurs in the entire file.
Example
Source file:
AABABC
ZZAACZCCA
QRAAUTUTA
In this example, in the first line the searched subsequence (ABA) has length 3, in the second line (ACZСA) and in the third line (AUTUTA) ; - length 6. We take the second line, because it is in the file before. In this subsequence, the letter C occurs most often, it occurs 4 times in the entire file. In the answer for this example, write C4.
Assignment file
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 minimum non-trivial divisors of an integer (excluding one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 20 000 000, in ascending order and looks among them for those for which the value M > 0 and even. Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 minimum non-trivial divisors of an integer (excluding one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 20 000 000, in ascending order and looks among them for those for which the value M > 0 and all digits of M are even. Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 minimum non-trivial divisors of an integer (excluding one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 20 000 000, in ascending order and looks among them for those for which the value M > 0 and all digits of M are odd. Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 4 non-trivial divisors of an integer - two minimum and two maximum (not counting the unit and the number itself). If the number does not have 4 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 20 000 000, in ascending order and looks among them for those for which the value M > 0 and digits of the number M form a non-decreasing sequence. Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 4 non-trivial divisors of an integer - two minimum and two maximum (not counting the unit and the number itself). If the number does not have 4 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 20 000 000, in ascending order and looks among them for those for which the value M > 17,000,000 and the decimal notation M ends in 35. Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 of the maximum non-trivial divisors of an integer (not counting one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 20 000 000, in ascending order and looks among them for those for which the value M > 20 000 000 and the sum of the digits of the number M is a multiple of 7. Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 of the maximum non-trivial divisors of an integer (not counting one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over integers greater than 20 000 000, in ascending order and looks among them for those for which the value M > 20 000 000 and the sum of the number formed by 3, 2 and 1 digits of M and the number formed by 6, 5 and 4 digits of M is a multiple of 5 (digits are counted from the end of the number, starting from 1).
For example, with М = 12345678 the number formed by 3, 2 and 1 digits - 678, the number formed by 6, 5 and 4 digits - 345.
Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in ascending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 of the maximum non-trivial divisors of an integer (not counting one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over the integers less than 20 000 000, in descending order and finds among them the first five such that the value 0 < M < 5 000 000 and the number formed by 3, 2 and 1 digits of the number M is not greater than the number formed by 6, 5 and 4 digits of the number M (digits are counted from the end of the number, starting from 1) .
For example, with М = 12345678 the number formed by 3, 2 and 1 digits - 678, the number formed by 6, 5 and 4 digits - 345.
Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in descending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 of the maximum non-trivial divisors of an integer (not counting one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over the integers less than 20 000 000, in descending order and finds among them the first 5 for which the value M > 10,000,000 and M is a multiple of its sum of digits.
Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in descending order of found numbers.
| |
![]()
|
|
Темы:
USE
Let M – the sum of 5 of the maximum non-trivial divisors of an integer (not counting one and the number itself). If the number does not have 5 non-trivial divisors, then the M value is considered equal to zero.
Write a program that iterates over the integers less than 20 000 000, in descending order and finds among them the first 5 for which the value 0 < M < 10 000 000 and in M there is only one even digit.
Print the first five found numbers and their corresponding values M.
Output format: for each of the five such found numbers in a separate line, the number itself is displayed first, then – value M (separated by one space). Lines are displayed in descending order of found numbers.
| |
![]()
|
|
Темы:
USE
Using sort
The planet Bluk is home to the largest super stadium in the galaxy. In the super stadium 10,000 rows, numbered starting from 1. In each row 10 000 places numbered starting from 1. To date, the Superstar concert has sold N tickets. The file contains information about sold tickets: row number and seat number in this row. Determine which row has the most vacant seats adjacent to each other. If there are the same number of such seats in several rows, then indicate the minimum number of the row. And also indicate the minimum number of the place from which such free places begin.
Input
The first line of the input file contains an integer N – the total number of tickets sold. Each of the following N lines contains 2 integers: the row number and the position number in this row.
In your answer, write down two integers: the number of the row that has the most empty seats next to it, then – the minimum number of the place from which such free places begin.
An example of the organization of the initial data in the input file (with 5 rows and 5 places in a row):
17
1 2
23
24
3 1
3 2
4 1
4 2
4 3
5 1
5 5
5 4
5 2
5 3
34
3 5
4 5
15
Response: 1 3
Assignment file
| |
![]()
|
|
Темы:
Count sort
USE
For the performance, the gymnasts use ribbons, which are placed on the table after the performance. The father of the best gymnast Anna K., in anticipation of the award, decided to write down the coordinates of the beginning and end of the ribbons. If the tape hung from the left edge of the table, then he set the left coordinate equal to zero, if the tape hung from the right end of the table, then he set the right coordinate equal to zero. If the tape hung from both sides, then he recorded both coordinates equal to zero. Do you have a file with this information. Determine how many points of the table turned out to be the largest thickness of the coating and what it is equal to. The table has a length Lmm. At the end of the performance of all the gymnasts, there was N tapes. Some ribbons have only one end hanging off the table, some have both. All tapes lie horizontally. The ribbons stack on top of each other.
Input
The first line of the file contains two numbers - L, N (1 <= L <= 10000, 1 <= N <= 10000). The following N lines contain 2 numbers each - l, r (1 <= l <= r <= L) - left and right ends of the tapes relative to the left edge of the table.
In your answer, indicate two numbers separated by a space - the maximum thickness of the tape table cover and the number of points with such a thickness.
| |
![]()
|
|
Темы:
Sorting algorithms
USE
Hearing that chocolate is good for the brain and nervous system, student Vasily decides to buy chocolate for the entire academic year. Vasily decided to buy chocolate for R rubles. He walked around in the city all N shops that sell various chocolates. Vasily saved to a file the information that in ith shop he can buy no more Bi bars of chocolate by < code>Ai rubles each.
A thrifty student wants to spend as much of his money as possible (preferably all at once) and buy as much chocolate as possible with it. Help Vasily figure out how many chocolate bars he can buy with his own money and how much the most expensive bar he can buy will cost.
Input
The first line in the file contains two numbers: N and R. The following N lines contain a pair of numbers: Ai and Bi.< br />
In your answer, write two numbers separated by a space on one line: first, the number of chocolate bars that Vasily can buy with his own money, then the cost of the most expensive chocolate bar that Vasily will have after the purchase.
Assignment file
| |
![]()
|
|
Темы:
USE
Using sort
Math lover Gosha came up with his own sequence. The rules in its sequence are:
1) all numbers in the sequence have their own number;
2) the first element of the sequence has number 1;
3) each number in the sequence must be divisible by its number;
4) the number with a larger number must be no less than the number with a smaller number.
An example of Gosha's sequence: 1 4 6 8 10 18 21.
Given a set of numbers, determine what is the maximum number of numbers that can be chosen to compose the Goshin sequence, as well as what is the maximum number that can be in it.
Input
The first line of the input file contains the number N - the number of numbers in the file. Next comes N natural numbers (N <= 105), each on a separate line.
Write down in your answer: first, the maximum number of numbers that can be chosen to make the Goshin sequence, then the maximum number that can be in this sequence.
Example input file:
12
25
17
20
15
6
9
10
12
5
3
4
1
Response: 5 25
Assignment file
| |
![]()
|
|
Темы:
Using sort
USE
Math lover Gosha came up with his own sequence. The rules in its sequence are:
1) all numbers in the sequence have their own number;
2) the first element of the sequence has number 1;
3) each number in the sequence must be divisible by its number;
4) the number with the larger number must be greater than the number with the smaller number.
An example of Gosha's sequence: 1 4 6 8 10 18 21.
Given a set of numbers, determine what is the maximum number of numbers that can be chosen to make the Goshin sequence, and also what is the maximum number that can be in it.
Input
The first line contains the number N - the number of numbers in the file (N <= 105). Next comes N natural numbers (no more than 106), each on a separate line.
Input
Print two space-separated numbers: first, the maximum number of numbers that can be chosen to make the Goshin sequence, then the maximum number that can be in this sequence.
Examples
| # |
Input |
Output |
| 1 |
12
25
17
20
15
6
9
10
12
5
3
4
1 |
5 25 |
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line four natural numbers. Find out how many quadruples of numbers can be sides of a rectangle. Write only the number in your answer.
Assignment file
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line four natural numbers.
Find out how many quadruples of numbers can be sides rectangle. Write only the number in your answer.
Assignment file
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line four natural numbers.
Find out how many quadruples of numbers can be sides square. Write only the number in your answer.
Assignment file
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line three natural numbers.
Find out how many triplets of numbers can be sides right triangle. Write only the number in your answer.
Assignment file
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line three natural numbers.
Find out how many lines have the sum of any two numbers equals the third number. Write only the number in your answer.
Assignment file
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line three natural numbers.
Find out how many lines have at least two the same numbers. Write only the number in your answer.
Assignment file
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line four natural numbers.
Find out how many lines have at least one a number with one digit. Write only the number in your answer.
Assignment file
| |
![]()
|
|
Темы:
USE
Open the spreadsheet file containing each line three natural numbers.
Find out how many triplets of numbers can be sides right triangle. In your answer, write down the minimum area of such a right triangle.
Assignment file
| |
![]()
|
|
Темы:
USE
The square is lined with N × N cells (1 < N < 30). The EM performer can move around the cells by performing one of two commands in one move: left or down. On command left EMU moves to the adjacent left cell, on command down – to the adjacent lower one. The square is bounded by external walls. There can also be internal walls between adjacent square cells. EMU cannot pass through walls.
At the initial moment of time, the EMU has a supply of fruits equal to the number written in the starting cell. When moving from cell to cell, EMU eats a certain number of fruits. When moving to the left, the EMU eats as many fruits as it is written in the cell to which it moves, plus 5 more. When moving down, the EMU eats the amount of fruit that is 2 times less than the number recorded in the cell to which it moves, and, at the same time, if the cell contains an even number, otherwise he eats only one fruit. Determine the maximum and minimum number of fruits that the EST has in stock by going from the top right square (starting square) to the bottom left.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 | |
![]()
|
|
Темы:
USE
Ralph, the hero of eight-bit computer games, got into a labyrinth of N × N cells (1 < N < 30). According to the rules of the maze, Ralph can navigate using three commands: left, down or jump. On command to the left Ralph moves to the adjacent cell to the left, on command down – to the next lower one, by command jump Ralph moves to the cell, which is located one to the left and two below the current cell (see example). The square is bounded by outer walls. There can also be internal walls between adjacent square cells. Ralph cannot walk through the walls, but he can jump over the innerwalls of the labyrinth with the jump command. Ralph can't go outside the labyrinth.
At the initial moment of time, Ralph has a star score equal to the number written in the starting cell. Each cell of the maze contains an integer. When moving from cell to cell, Ralph's score changes to the number that is written in the cell to which he moves. At the same time, if the number is positive, then the score increases, if it is negative, it decreases.
Determine the maximum and minimum star scores if Ralph starts from the top right cell and ends at the bottom left.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
Example of moving Ralph with the command jump
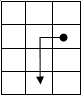
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
| |
![]()
|
|
Темы:
USE
Ralph, the hero of eight-bit computer games, got into a labyrinth of N × N cells (1 < N < 30). According to the rules of the maze, Ralph can navigate using three commands: right, up , or jump. On command to the right Ralph moves to the neighboring right cell, on command up – to the adjacent upper one, by command jump Ralph moves to the cell, which is located one to the right and two higher from the current cell (see example). The square is bounded by outer walls. There can also be internal walls between adjacent square cells. Ralph cannot walk through the walls, but he can jump over the innerwalls of the labyrinth with the jump command. Ralph can't go outside the labyrinth.
At the initial moment of time, Ralph has a star score equal to the number written in the starting cell. Each cell of the maze contains an integer. When moving from cell to cell, Ralph's score changes to the number that is written in the cell to which he moves. At the same time, if the number is positive, then the score increases, if it is negative, it decreases.
Determine the maximum and minimum star scores if Ralph starts from the bottom left cell and ends at the top right.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
Example of moving Ralph with the command jump
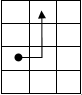
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
| |
![]()
|
|
Темы:
USE
Ralph, the hero of eight-bit computer games, got into a labyrinth of N × N cells (1 < N < 30). According to the rules of the maze, Ralph can navigate using two commands: right or up. On command to the right Ralph moves to the neighboring right cell, on command up – to the next upper one. The square is bounded by outer walls. There can also be internal walls between adjacent square cells. Ralph cannot go through walls. Ralph can't go outside the labyrinth either.
In each cell of the maze, Ralph eats a certain number of pancakes. In the starting cell, he also eats pancakes. The number of pancakes Ralph eats is determined by the rules of the maze. If the number indicated in the cell is even, then Ralph eats half of the indicated number, otherwise, he eats all the pancakes.
Determine the maximum and minimum number of pancakes that Ralph will eat by moving from the lower left cell (starting cell) to the upper right one.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 | |
![]()
|
|
Темы:
USE
Ralph, the hero of eight-bit computer games, got into a labyrinth of N × N cells (1 < N < 30). According to the rules of the maze, Ralph can navigate using two commands: right or down. On command to the right Ralph moves to the neighboring right cell, on command down – to the next lower one. The square is bounded by outer walls. There can also be internal walls between adjacent square cells. Ralph cannot go through walls. Ralph can't go outside the labyrinth either.
In each cell of the maze, Ralph eats a certain number of pancakes. In the starting cell, he also eats pancakes. The number of pancakes Ralph eats is determined by the rules of the maze. If the number indicated in the cell is a multiple of three, then Ralph eats a third of the indicated number, otherwise, he eats only one pancake.
Determine the maximum and minimum number of pancakes that Ralph will eat by moving from the top left cell (starting cell) to the lower right.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 | |
![]()
|
|
Темы:
USE
Ralph, the hero of eight-bit computer games, got into a labyrinth of N × N cells (1 < N < 30). According to the rules of the maze, Ralph can move using three commands: right, down or oblique. By command right Ralph moves to the neighboring right cell, by command down – to the adjacent lower, on command & nbsp; obliquely - to the next cell diagonally to the right and down. The square is bounded by outer walls. There can also be internal walls between adjacent square cells. Ralph cannot go through walls. Ralph can't go outside the labyrinth either.
In each cell of the maze, Ralph eats a certain number of pancakes. In the starting cell, he also eats pancakes. The number of pancakes Ralph eats is determined by the rules of the maze. If the number indicated in the cell ends in 5, then Ralph eats a fifth of all the pancakes, otherwise, he eats all the pancakes.
Determine the maximum and minimum number of pancakes that Ralph will eat by moving from the top left cell (starting cell) to the lower right.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 | |
![]()
|
|
Темы:
USE
Ralph, the hero of eight-bit computer games, got into a labyrinth of N × N cells (1 < N < 30). According to the rules of the maze, Ralph can navigate using three commands: left_1, left_2, or up. By command left_1 Ralph moves to the adjacent left cell, by command left_2 – through one cell to the left, on command & nbsp; up - to the next cell above. The square is bounded by outer walls. There can also be internal walls between adjacent square cells. Ralph cannot go through walls. Ralph can't go outside the labyrinth either.
Each cell of the maze contains an integer. Getting into each cell, Ralph updates his score by the value of the number written in the cell in which he falls. Moreover, if the number written in the cell is positive, then Ralph's score increases, if negative, it decreases. Ralph's starting score is written in the starting square.
Determine the maximum and minimum score that Ralph will have when moving from the lower right cell of the labyrinth (starting cell) to the upper left.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 | |
![]()
|
|
Темы:
USE
Ralph, the hero of eight-bit computer games, got into a labyrinth of N × N cells (1 < N < 30). According to the rules of the maze, Ralph can navigate using three commands: left_1, left_2, or up. By command left_1 Ralph moves to the adjacent left cell, by command left_2 – through one cell to the left, on command & nbsp; up - to the next cell above. The square is bounded by outer walls. There can also be internal walls between adjacent square cells. Ralph cannot go through walls. Ralph can't go outside the labyrinth either.
Each cell of the maze contains an integer. Getting into each cell, Ralph updates his score by the value of the number written in the cell in which he falls. Moreover, if the number written in the cell is positive, then Ralph's score increases, if negative, it decreases. Ralph's starting score is recorded in the starting cell. Cells with a green highlighted background are bonus. When passing through these cells, Ralph's score increases by 10 times the number written in it. Cells with a red highlighted background are penalty. When passing through these cells, Ralph's score decreases by a number 10 times greater than that written in it.
Determine the maximum and minimum score that Ralph will have when moving from the lower right cell of the labyrinth (starting cell) to the upper left.
Answer two numbers – first the maximum number, then the minimum. Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 | |
![]()
|
|
Темы:
USE
The square is lined with N × N cells (1 < N < 30). The executor Robot can move around the cells, performing one of two commands for one movement: right or up. On command to the right the Robot moves to the adjacent right cell, on command up – to the next upper one. The square is bounded by outer walls. There can also be internal walls between adjacent cells of a square. The robot cannot pass through the wall.
Before each start of the Robot, in each cell of the square there is a coin with a value from 1 to 100. Having visited the cell, the Robot takes the coin with him; this also applies to the start and end cells of the Robot's route.
Determine the maximum and minimum amounts of money that the Robot can collect by going from the bottom left cell to the top right. Answer two numbers – first the maximum amount, then the minimum.
The source data is a spreadsheet of size N × N, each cell of which corresponds to a square cell. The inner and outer walls are marked with thick lines.
Sample input
For the specified input, the answer should be a pair of numbers: 22 34
Assignment file
| |
![]()
|
|
Темы:
Information encoding
USE
To encode a certain sequence consisting of all capital letters of the Russian alphabet, we decided to use a non-uniform binary code that satisfies the condition that no code word is the beginning of another code word. This condition ensures that encoded messages can be unambiguously decrypted. The code words of the first letters of the alphabet are known: A - 00, B - 01. What is the smallest length of the GROMOZEKA subsequence code?
| |
![]()
|
|
Темы:
Information encoding
USE
To encode a certain sequence consisting of all capital letters of the Russian alphabet, we decided to use a non-uniform binary code that satisfies the condition that no code word is the beginning of another code word. This condition ensures that encoded messages can be unambiguously decrypted. Known code words some letters of the alphabet: B - 010, C - 011. What is the smallest length of the KAMCHATKA subsequence code?
| |
![]()
|
|
Темы:
Information encoding
USE
To encode a certain sequence consisting of all capital letters of the Russian alphabet, we decided to use a non-uniform binary code that satisfies the condition that no code word is the beginning of another code word. This condition ensures that encoded messages can be unambiguously decrypted. The code words of the first letters of the alphabet are known: A - 00, B - 01. The remaining letters are encoded in such a way that the code of the subsequence GROMOZEKA has the smallest possible length. Specify the shortest possible code word for the letter O , in which the code will satisfy the specified condition. If there is more than one such code, indicate the code with the smallest numerical value.
| |
![]()
|
|
Темы:
USE
Cycles
Given a sequence of N natural numbers. All its continuous subsequences starting from the first element of the sequence are considered. Find the number of subsequences whose sum is a multiple of K.
Input
The first line contains two numbers: the number of numbers in the sequence N (1 <= N <= 108) and the number K ( 1 <= K <= 100). Next comes N lines, one natural number per line. Each number does not exceed 10000.
Imprint
Display the answer to the problem
Examples
| # |
Input |
Output |
| 1 |
5 3
33
41
19
22
40 |
2 |
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \(\neg {(w \rightarrow x)} \wedge ((y \equiv z) \vee y \wedge \bar z)\). At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
| ? |
? |
? |
? |
F |
| |
|
1 |
0 |
1 |
| |
|
|
1 |
1 |
| 1 |
|
0 |
|
1 |
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \(y \wedge (x \neq w) \wedge (z \rightarrow x)\). At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
| ? |
? |
? |
? |
F |
| |
0 |
0 |
|
1 |
| 1 |
0 |
|
0 |
1 |
| 1 |
|
|
1 |
1 |
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \((y=z) \vee \bar y \wedge (x \vee w) \vee \neg (w \rightarrow \bar y)\) . At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
| ? |
? |
? |
? |
F |
| |
1 |
0 |
|
0 |
| 0 |
1 |
1 |
0 |
0 |
| 0 |
|
|
1 |
0 |
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \(w \rightarrow (x \wedge \bar y \vee (y \equiv z))\). At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
| ? |
? |
? |
? |
F |
| |
1 |
0 |
1 |
0 |
| |
1 |
1 |
1 |
0 |
| 1 |
|
|
0 |
0 |
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \((z \rightarrow (x \wedge w))\vee \bar w \wedge (x \rightarrow y)\). At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
| ? |
? |
? |
? |
F |
| 0 |
|
0 |
|
0 |
| |
|
1 |
|
0 |
| 0 |
|
|
0 |
0 |
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
Yura Barankin filled in the truth table of the function \(\neg (z \rightarrow x)\wedge(w\rightarrow y)\). At the moment when Kostya called him out for a walk, Yura managed to fill in only a fragment of three different rows of the table. After the walk, Yura noticed that he had not indicated which column of the table each of the variables w, x, y, z corresponds to.
| ? |
? |
? |
? |
F |
| |
0 |
|
|
1 |
| |
|
0 |
1 |
1 |
| |
1 |
|
0 |
1 |
Help Yura restore the table columns. Specify which column each of the variables w, x, y, z corresponds to.
In your answer, write the letters w, x, y, z in the order of their corresponding columns (first the letter corresponding to the first column; then the letter corresponding to the second column, etc.). Write the letters in the answer in a row, no separators between the letters are needed.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 319 characters and containing only decimal digits and characters from the 4540-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 32768 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 161 characters and containing only decimal digits and characters from the 3134-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 65536 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 388 characters and containing only decimal digits and characters from the 3464-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 65536 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 364 characters and containing only decimal digits and characters from the 2773-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 32768 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 299 characters and containing only decimal digits and characters from the 3540-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 4096 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 144 characters and containing only decimal digits and characters from the 1436-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 8192 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 259 characters and containing only decimal digits and characters from the 2489-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 32768 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 340 characters and containing only decimal digits and characters from the 3916-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 8192 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 203 characters and containing only decimal digits and characters from the 1977-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 8192 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Measuring Information
When registered in a computer system, each object is assigned an identifier consisting of 215 characters and containing only decimal digits and characters from the 4483-character alphabet. In the database, each identifier is stored in the same and the minimum possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the amount of memory (in KB) required to store 4096 identifiers. In the answer, write down only an integer - the number of KB.
| |
![]()
|
|
Темы:
USE
Strings
The text file consists of no more than 106 characters and contains only uppercase Latin letters (ABC…Z). The text is divided into lines of various lengths. We call a subsequence original if it is bounded on the left by the substring AB, and on the right by the substring BA (these substrings are also included in the subsequence) and there are no other letters in this subsequence A and B. The original subsequence cannot start on one line and end on another.
Determine how much total original subsequences in the entire file, as well as the length of the maximum of them.
In your answer, write together two integers, first the number of original subsequences, then the length of the maximum of them.
Example
Source file:
AAABCAABCBAA
ZZABZZZBABCBA
QRABUTUUBA
There are 4 original subsequences in this example (ABUTUTBA, ABZZZBA, ABCBA, ABUTUTBA)
The longest subsequence (ABUTUTBA) has a length of 8.
Answer: 48
Assignment file
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3 \cdot 8^{112} - 2\cdot8 ^{78}+4\cdot8^{63}- 2 \cdot 8^{35}-8^{8} -52\)
written in the number system with base 8. How many digits other than 7, are in this entry?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(2 \cdot 4^{84} + 3\cdot4 ^{42}- 2\cdot4^{34}+ 2 \cdot 4^{17}+3\cdot 4^{3} +16\)
written in the number system with base 4. How many adjacent numbers "20" contained in this post?
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(25^{4848} - 2\cdot25 ^{4090}- 2\cdot5^{4556}- 4 \cdot 5^{2276}-5^{4404} -5^{4313}+13320\)
written in the number system with base 5. How many adjacent pairs of numbers "41" contained in this post?
| |
![]()
|
|
Темы:
USE
Logic and sets
Let us denote by DIV(n, m) the statement "a natural number n is divisible without remainder by a natural number m". For what is the smallest natural number A< /code> boolean expression
\((DIV(x, 7) \rightarrow \neg DIV(x, 10)) \vee (x+A\ geq 100)\)
identically true (i.e. takes the value 1) for any integer natural value of the variable х.
| |
![]()
|
|
Темы:
USE
Logic and sets
Let us denote by DIV(n, m) the statement "a natural number n is divisible without remainder by a natural number m". For what is the smallest natural number A< /code> boolean expression
\((x \geq 8) \rightarrow ( \neg DIV(x, 3) \rightarrow DIV(x, 2)) \vee (x+A\geq 25)\)
identically true (i.e. takes the value 1) for any integer natural value of the variable х.
| |
![]()
|
|
Темы:
USE
Logic and sets
Let us denote by DIV(n, m) the statement "a natural number n is divisible without remainder by a natural number m". For what is the largest natural number A< /code> boolean expression
\((DIV(x, 7) \rightarrow \neg DIV(x, 10)) \vee (x-A\geq 10 )\)
identically true (i.e. takes the value 1) for any integer natural value of the variable х.
| |
![]()
|
|
Темы:
USE
Logic and sets
Let us denote by DIV(n, m) the statement "a natural number n is divisible without remainder by a natural number m". For what is the largest natural number A< /code> boolean expression
\((x \geq 15) \rightarrow ( \neg DIV(x, 3) \rightarrow DIV(x, 2)) \vee (x-A\geq 10)\)
identically true (i.e. takes the value 1) for any integer natural value of the variable х.
| |
![]()
|
|
Темы:
USE
Logic and sets
Let us denote by DIV(n, m) the statement "a natural number n is divisible without remainder by a natural number m". For what is the smallest natural number A< /code> boolean expression
\((x < 100) \rightarrow ((\neg DIV(x, 3) \wedge \neg DIV(x , 4))\rightarrow DIV(x, 5)) \vee (x+A\geq 60)\)
identically true (i.e. takes the value 1) for any integer natural value of the variable х.
| |
![]()
|
|
Темы:
USE
Logic and sets
Let us denote by DIV(n, m) the statement "a natural number n is divisible without remainder by a natural number m". For what is the largest natural number A< /code> boolean expression
\((x < 100) \rightarrow (( DIV(x, 3) \wedge DIV(x, 4)) \rightarrow \neg DIV(x, 5)) \vee (x-A\geq 25)\)
identically true (i.e. takes the value 1) for any integer natural value of the variable х.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 1;
F(n) = 15 + f(n/3) if n > 0, and the number n is a multiple of 3;
F(n) = 7 + f(n/2) otherwise.
Determine how many distinct values n, belonging to the segment [1, 1000000], the function F(n)=137?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 12;
F(n) = 21 + f(n/5) if n > 0, and the number n is a multiple of 5;
F(n) = 1 + f(n/2) otherwise.
Determine how many distinct values n, belonging to the segment [1, 1000000], the function F(n)=37?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 12;
F(n) = 1 + f(n/15) if n > 0, and the number n is a multiple of 15;
F(n) = 1 + f(n/30) otherwise.
Determine how many different values the F(n) function takes on the segment [1, 1000000]?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 12;
F(n) = 1 + f(n/3) if n > 0, and the number n is a multiple of 3;
F(n) = 1 + f(n/15) otherwise.
Determine how many different values the F(n) function takes on the segment [1, 1000000]?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = -1;
F(n) = f(n-1) + f(n/4) if n > 0, and the number n is a multiple of 4;
F(n) = f(n/5) otherwise.
Determine how many distinct values n, belonging to the segment [1, 1000000], the function F(n)=-50?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – non-negative number, is given by the following relations:
F(0) = 5;
F(n) = n/3 + f(n/15) if n > 0, and the number n is a multiple of 15;
F(n) = n + 1 + f(n/2) otherwise.
Determine how many distinct values n, belonging to the segment [1, 1000000], the value F(n) is less than 100?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 5;
F(n) = n/15 + f(n/3) if n > 0, and the number n is a multiple of 15;
F(n) = f(n-1) otherwise.
Determine how many distinct values n, belonging to the segment [1, 1000000], value F(n) less than 100?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 5;
F(n) = n/20 + f(n/8) if n > 0, and the number n is a multiple of 40;
F(n) = f(n/20) otherwise.
Determine how many distinct values n, belonging to the segment [1, 1000000], the function F(n)=175?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 15;
F(n) = n/5 + f(n/2) if n > 0, and the number n is a multiple of 20;
F(n) = f(n/3) otherwise.
Determine how many different values the F(n) function takes on the segment [1, 1000000]?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(0) = 7;
F(n) = n/7 + f(n/7) if n > 0, and the number n is a multiple of 7;
F(n) = f(n-1) otherwise.
Determine how many different values the F(n) function takes on the segment [1, 1000000]?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – non-negative number, is given by the following relations:
F(0) = 9;
F(n) = n/3 + f(n/3) if n > 0, and the number n is a multiple of 9;
F(n) = n/2 + f(n/2) otherwise.
Determine how many different values the F(n) function takes on the segment [1, 1000000]?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n if n < 100;
F(n) = n + F(n/3), otherwise;
G(n) = n + 1 if n < 100;
G(n) = G(F(n/2)) otherwise.
Determine how many different values the G(n) function takes on the segment [100, 100000]?
The sign / - means the operation of integer division.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n if n < 100;
F(n) = n + F(n/3), otherwise;
G(n) = n + 1 if n < 100;
G(n) = G(F(n/2)) otherwise.
Determine how many distinct values n, belonging to the segment [100, 100000], the function G(n)=99?
The sign / - means integer division operation.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n + 10 if n < 10;
F(n) = n % 10 + G(F(n/10)), otherwise;
G(n) = n + 10 if n < 10;
G(n) = n % 10 + G(n/10), otherwise;
Determine how many different values the F(n)function takes for all n smaller 1000000?
Sign / - means integer division operation.
Sign % - means the operation of calculating the remainder of the division of two integers.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n + 10 if n < 10;
F(n) = n % 10 + G(F(n/10)), otherwise;
G(n) = n + 10 if n < 10;
G(n) = n % 10 + G(n/10), otherwise;
Determine how many different values n smaller 1000000, function F(n)=25?
The sign / - means integer division operation.
The sign % - means the operation of calculating the remainder when dividing two integers.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n + 10 if n < 10;
F(n) = n % 10 + G(F(n/10)), otherwise;
G(n) = n + 10 if n < 10;
G(n) = n % 10 + G(n/10), otherwise;
Define the minimum value n, where the function F(n)=30?
The sign / - means integer division operation.
The sign % - means the operation of calculating the remainder when dividing two integers.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n + 10 if n < 10;
F(n) = n % 10 + G(F(n/10)), otherwise;
G(n) = n + 10 if n < 10;
G(n) = n % 10 + G(n/10), otherwise;
Determine the sum of all values of the function F(n) for all values n smaller 1000000?
The sign / - means integer division operation.
The sign % - means the operation of calculating the remainder when dividing two integers.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n % 10 if n < 100;
F(n) = n / 100 + G(n%100), otherwise;
G(n) = n % 10 if n < 100;
G(n) = n % 100 + F(n/100), otherwise;
Determine the sum of all values of the function F(n), for all values n smaller 100000?
The sign / - means integer division operation.
The sign % - means the operation of calculating the remainder when dividing two integers.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – non-negative integer, is given by the following relations:
F(n) = n % 10 if n < 100;
F(n) = n / 100 + G(n%100), otherwise;
G(n) = n % 10 if n < 100;
G(n) = n % 100 + F(n/100), otherwise;
Determine the sum of all function values G(n), for all values n smaller 100000?
The sign / - means integer division operation.
The sign % - means the operation of calculating the remainder when dividing two integers.
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the functions F(n) and G(n), where n – natural number, given by the following relations:
F(n) = n + 10 if n < 10;
F(n) = n % 10 + G(F(n/10)), otherwise;
G(n) = n + 10 if n < 10;
G(n) = n % 10 + G(n/10), otherwise;
Determine the number of distinct values n, not exceeding 106, for which function F(n) is a multiple of 7?
The sign / - means integer division operation.
The sign % - means the operation of calculating the remainder when dividing two integers.
| |
![]()
|
|
Темы:
USE
The figure shows a diagram of the roads of a certain region of the region in the form of a graph, the table shows the length of these roads in kilometers. The table and the diagram were drawn independently of each other, the numbering of the items in the table is in no way connected with the letter designations on the graph. Determine the sum of the side lengths between point A and point B, and between point F and point G. ;Reply with an integer – as it is indicated in the table.
| |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
P7 |
| P1 |
x |
|
11 |
|
10 |
7 |
|
| P2 |
|
x |
10 |
|
|
8 |
|
| P3 |
11 |
10 |
x |
|
13 |
|
|
| P4 |
|
|
|
x |
|
13 |
3 |
| P5 |
10 |
|
13 |
|
x |
|
5 |
| P6 |
7 |
8 |
|
13 |
|
x |
|
| P7 |
|
|
|
3 |
5 |
|
x |
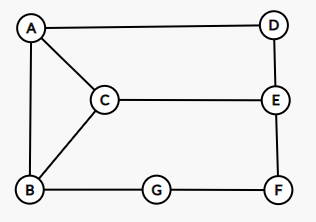
| |
![]()
|
|
Темы:
USE
Measuring Information
When registering in a computer system, each object is assigned an identifier consisting of 250 characters. The identifier can contain decimal digits and characters from a special set of 1560 characters. The database stores information about each identifier with the same and the smallest possible integer number of bytes. In this case, character-by-character encoding of identifiers is used, all characters are encoded with the same and the minimum possible number of bits.
Determine the minimum amount of memory, in KB, that must be allocated to store identities for 32768 users.
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3\cdot 16^{2018} - 2\cdot 8 ^{1028}- 3\cdot4^{1100} - 2^{1050}-2022\)
written in the number system with base 4. How many triples are there in this entry?
| |
![]()
|
|
Темы:
USE
The algorithm for calculating the value of the function F(n), where n – natural number, given by the following relations:
F(n) = 2 if n < 3;
F(n) = F(n - 1) + F(n - 2) - n if n > 2 and n even;
F(n) = F(n - 2) - F(n - 1) + 2n if n > 2 and n odd.
Determine what is the value of the function F(30)?
Write only an integer in your answer.
| |
![]()
|
|
Темы:
USE
The square is lined with N × N cells (1 < N < 30). The Executor Robot can move around the cells by performing one of two commands in one move: right or down. right command moves to the neighboring right cell, down – to the lower one.
The square is bounded by outer walls. There can also be internal walls between adjacent square cells. The robot cannot pass through walls.
Before each start of the Robot, in each cell of the square there is a coin with a value from 1 to 100. Having visited the cell, the Robot takes the coin with him; this also applies to the start and end cells of the Robot's route.
Determine the maximum and minimum amounts of money that the Robot can collect by going from the upper left cell to the lower right. In your answer, indicate two numbers – first the maximum amount, then the minimum.
Both numbers are specified on the same line, separated by one space.
The source data is a spreadsheet of N × N, each cell of which corresponds to a square cell. Inner & nbsp; outer walls are marked with thick lines.
 For the specified input, the answer must be a pair of numbers
38 22
| |
![]()
|
|
Темы:
USE
In the figure, the road map of a certain area is shown as a graph; in the table, an asterisk indicates the presence of a road between settlements. Since the table and the diagram were drawn independently of each other, the numbering of settlements in the table is in no way connected with the letter designations on the graph. Determine the numbers of points D and E, write down the found numbers in ascending order without separators. For example, if the answer were points P1 and P6, then 16 would have to be indicated as an answer.
If there are several possible answers, indicate the one that has the lower numerical value.
| |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
| P1 |
x |
* |
|
|
* |
* |
| P2 |
* |
x |
* |
|
|
* |
| P3 |
|
* |
x |
* |
* |
|
| P4 |
|
|
* |
x |
* |
* |
| P5 |
* |
|
* |
* |
x |
|
| P6 |
* |
* |
|
* |
|
x |
| |
![]()
|
|
Темы:
USE
In the figure, the road map of the N district is shown as a graph, the table contains information about the length of each of these roads (in kilometers). Since the table and the diagram were drawn independently of each other, the numbering of settlements in the table has nothing to do with the lettering on the graph. Determine the sum of the lengths of roads from point C to point D and from point E to point F.
Write an integer as your answer.
| |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
P7 |
| P1 |
x |
27 |
24 |
|
|
|
|
| P2 |
27 |
x |
21 |
|
18 |
|
|
| P3 |
24 |
21 |
x |
15 |
12 |
9 |
30 |
| P4 |
|
|
15 |
x |
|
33 |
|
| P5 |
|
18 |
12 |
|
x |
|
36 |
| P6 |
|
|
9 |
33 |
|
x |
39 |
| P7 |
|
|
30 |
|
36 |
39 |
x |
| |
![]()
|
|
Темы:
USE
Number systems
The value of an arithmetic expression
\(3\cdot 216^{18} - 2\cdot 36 ^{10}- 3\cdot6^{9} - 2\)
written in the number system with base 6. How many 5 digits are in this entry?
| |
![]()
|
|
Темы:
USE
The square is lined into NxN cells (1 < N < 17). The Executor Robot can move around the cells by performing one of four commands in one move: right, down, right by 2 , down 2. On a command to the right, the Robot moves to the adjacent right cell, on a command down – to the next lower one. On a command to the right by 2 - to the cell located two cells to the right, and on a command down to 2 - to the cell located two cells below.
The square is bounded by outer walls. There can also be internal walls between adjacent cells of a square. The robot cannot pass through the wall. Before each start of the Robot, in each cell of the square there is a coin with a value from 1 to 100. Having visited the cell, the Robot takes the coin with him; this also applies to the start and end cells of the Robot's route.
Determine the maximum and minimum amounts of money that the Robot can collect by going from the upper left cell to the lower right one. Answer two numbers — first the maximum amount, then the minimum.
The source data is a spreadsheet of size N × N, each cell of which corresponds to a square cell. The inner and outer walls are marked with thick lines.
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 67 [Forward 10 Right 20]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 76 [Forward 5 Right 6]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 70 [Forward 10 Right 9]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 60 [Forward 10 Right 18]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 54 [Forward 7 Right 90]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 33 [Forward 8 Right 24]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 69 [Forward 6 Right 12]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 46 [Forward 9 Right 90]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 77 [Forward 10 Right 12]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine the number of segments that make up the figure given by the following algorithm:
Repeat 116 [Forward 9 Right 4]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 58 [Forward 5 Right 40]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 49 [Forward 5 Right 36]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 45 [Forward 3 Right 40]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 39 [Forward 3 Right 45]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 34 [Forward 5 Right 72]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 23 [Forward 3 Right 45]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 42 [Forward 4 Right 36]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 40 [Forward 4 Right 90]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 36 [Forward 3 Right 90]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the appropriate direction, Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise respectively.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
Determine how many points with integer positive coordinates will be inside the area bounded by the line defined by the following algorithm (without taking into account points on the line):
Repeat 21 [Forward 4 Right 36]
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 6 [Forward 4 Right 90 Forward 5 Right 90]
Raise your tail
Forward 3 Right 90 Forward 1 Left 90
Lower your tail
Repeat 12[Forward 10 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 2 [Forward 2 Right 90 Forward 9 Right 90]
Raise your tail
Forward 1 Right 90 Forward 1 Left 90
Lower your tail
Repeat 4[Forward 9 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 2 [Forward 4 Right 90 Forward 7 Right 90]
Raise your tail
Forward 4 Right 90 Forward 2 Left 90
Lower your tail
Repeat 4[Forward 9 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 2 [Forward 8 Right 90 Forward 5 Right 90]
Raise your tail
Forward 1 Right 90 Forward 3 Left 90
Lower your tail
Repeat 4[Forward 8 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 4 [Forward 8 Right 90 Forward 9 Right 90]
Raise your tail
Forward 2 Right 90 Forward 4 Left 90
Lower your tail
Repeat 8[Forward 10 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 4 [Forward 9 Right 90 Forward 1 Right 90]
Raise your tail
Forward 3 Right 90 Forward 2 Left 90
Lower your tail
Repeat 8[Forward 8 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 2 [Forward 9 Right 90 Forward 6 Right 90]
Raise your tail
Forward 2 Right 90 Forward 1 Left 90
Lower your tail
Repeat 4[Forward 9 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 4 [Forward 9 Right 90 Forward 2 Right 90]
Raise your tail
Forward 5 Right 90 Forward 5 Left 90
Lower your tail
Repeat 8[Forward 9 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 6 [Forward 1 Right 90 Forward 8 Right 90]
Raise your tail
Forward 5 Right 90 Forward 5 Left 90
Lower your tail
Repeat 12[Forward 8 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|
|
Темы:
USE
The performer Turtle acts on a plane with a Cartesian coordinate system. At the initial moment, the Turtle is at the origin of coordinates, its head is directed along the positive direction of the y-axis, the tail is lowered. With the tail lowered, the Turtle leaves a trail in the form of a line on the field. At each specific moment, the position of the performer and the direction of his movement are known.
The performer has commands: Forward n and Back n (where n – is an integer), causing the Turtle to move by n units in the corresponding direction; Right m and Left m (where m – is an integer) causing the direction to change to m degrees clockwise or counterclockwise, respectively; Raise tail, indicating the transition to move without drawing; Lower tail, indicating the transition to paint mode.
Recording
Repeat k [Command1 Command2 … CommandS]
means that the sequence of S commands will be repeated k times.
The turtle was given the following algorithm to execute:
Repeat 6 [Forward 10 Right 90 Forward 9 Right 90]
Raise your tail
Forward 3 Right 90 Forward 2 Left 90
Lower your tail
Repeat 12[Forward 7 Left 90]
Determine how many points with integer coordinates will be inside the intersection of shapes bounded by the lines specified by the algorithm, including points on the boundaries of this intersection:
| |
![]()
|