| Problem description | | Progress |
|
Темы:
Cycles
M soldiers are taking part in the parade. The parade command decided that the most spectacular formation of the military – in the form of a square, that is, the number of participants in the construction
should be an exact square. But since the number M may not be an exact square, it is allowed to divide the military into several regiments, each of which is built in the form
square. For beauty, all regiments should be the same size, and the parade command also wants the size of each regiment to be as large as possible. Determine the maximum possible shelf size.
The program receives as input one positive integer M, not exceeding 2×109, – the number of participants in the parade. The program should output one number – maximum shelf size.
| |
![]()
|
|
Темы:
Cycles
Vasya writes NxN natural numbers in order into the cells of the square table, first filling in the first row from left to right, then the second, and so on. (see picture on the left). Petya fills in the same table, placing the numbers first in the first column from top to bottom, then in the second column, and so on.
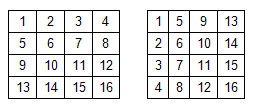
At the same time, it turned out that both Vasya and Petya wrote some numbers in the same cell (for example, the number 6 is written in the second line of the second column of both tables).
You need to write a program that outputs all numbers that are written in the same cells in both tables.
Input
One number is entered - the size of the table.
Imprint
The program should display all the numbers that are in the same place in both tables, in ascending order, separated by a space.
The size of the table is a natural number not exceeding 100.
Examples
| # |
Input |
Output |
| 1 |
4 |
1 6 11 16 |
| |
![]()
|
|
Темы:
Cycles
Two grasshoppers are sitting on a straight path at a distance of 1 meter from each other. From time to time one of the grasshoppers jumps a few centimeters to the left or right. It is required to find out what was the minimum distance that the grasshoppers approached in the process of jumping. (The distance is considered only in those moments when both grasshoppers are sitting on the ground).
Input: The first line contains a single number N (1 <= N <= 100) – the total number of jumps followed by N numbers describing the jumps. The modulus of the number is equal to the length of the jump in centimeters; the number is negative if the grasshopper started this jump towards another grasshopper, and positive – if from another grasshopper. The modulo numbers do not exceed 100 and all are different from 0. (Grasshoppers can jump over each other. Grasshoppers are guaranteed not to land on top of each other.)
Output: You need to output one number – the minimum distance in centimeters that grasshoppers approached.
Examples
| # |
Input |
Output |
| 1 |
5
1
2
3
4
5 |
100 |
| |
![]()
|
|
Темы:
Cycles
You need to draw a herringbone height on the screen H.
Input: Input one natural number H not exceeding 20.
Output: Draw a Christmas tree from asterisks (see examples).
Examples
| # |
Input |
Output |
| 1 |
2 |
*
***
|
| 2 |
4 |
*
***
*****
*******
|
| |
![]()
|
|
Темы:
for loop
while loop
Cycles
Two numbers N and K are entered. Print the number of numbers from 1 to N (inclusive) such that their sum of digits is divisible by K.
Examples
| # |
Input |
Output |
| 1 |
100 3 |
33 |
| 2 |
22 4 |
5 |
| |
![]()
|
|
Темы:
Cycles
The board game uses cards with numbers from 1 to N (N – natural number not exceeding 106). One card is missing. Find her.
Input: Given N, then N-1 numbers of remaining cards.
Output: Required to display lost card number.
Examples
| # |
Input |
Output |
| 1 |
5
1
2
3
4 |
5 |
| 2 |
4
3
2
4 |
1 |
| |
![]()
|
|
Темы:
Cycles
Strings
The path to the treasure is set in the form of indications of how many steps you need to go in one of the four directions: north (N), south (S), west (W), east (E). The entire route is written as a string containing a sequence of numbers followed by letters indicating the direction of movement. For example, the string "7N5E2S3E" means "walk 7 paces north, 5 paces east, 2 paces south, 3 paces east". A route can have many move commands, so each such route can be abbreviated.
For example, the previously given route can be shortened to "5N8E". For the given route to the treasure, shorten it to a string of minimum length.
The program receives as input a string consisting of non-negative integers, not exceeding 107 each, and one letter (N, S, W, E ) following each
number. There are no other characters (including spaces) in the string except numbers and direction letters. The string length does not exceed 250 characters. It is guaranteed that the initial
and the end point of the route are different.
The program should output a route leading to the same point, written in the same form as in the input, using the minimum number of characters. If answers
several, the program should display one (any) of them.
| Input |
Output |
Note |
| 7N5E2S3E |
5N8E |
The correct answer would also be "8E5N" |
| 10N30W20N |
30N30W |
The correct answer would also be "30W30N" |
| |
![]()
|
|
Темы:
Cycles
Given N integers. Find the second largest element of the sequence (the element that would be the penultimate if the input data were sorted non-decreasingly)
Input:
the first line sets the number N (\(2<=N<=10^5\))
then there are N lines, one integer in each line
Output:
print the second maximum element
Examples
| № |
Input |
Output |
| 1 |
7
10
15
20
35
14
35
10 |
35 |
| 2 |
5
10
5
7
11
9 |
10 |
| |
![]()
|
|
Темы:
Cycles
Bust
In some card game, a deck is used, in which there are 4 aces. 4 players take part in the game, each of which is dealt an equal number of cards, and two cards are put aside.
Each player boasted how many aces he had. Determine how many players knowingly lied.
For example, they said 1, 1, 1, 2. Therefore, 1 player obviously lied. (Some three could tell the truth, but all four could not tell the truth, since there are only 4 aces).
Input
4 numbers are entered (from 0 to 9 each), separated by a space – the number of aces according to the first, second, third and fourth players.
Imprint
Print one number – the minimum number of players who knowingly lied. If everyone could tell the truth at the same time, print the number 0.
Examples
| # |
Input |
Output |
| 1 |
1 1 1 2 |
1 |
| 2 |
1 1 1 1 |
0 |
| |
![]()
|
|
Темы:
Conditional operator
Cycles
In the younger group of the kindergarten "Teletubbies" there are n children in total. Each of them, like any four-year-old, can easily start crying simply because his classmates also cry. So what if he doesn't know what's wrong? Comrades can't be wrong.
The teacher has been working in the kindergarten for many years, and is well versed in the children's mood. It is enough for her to look at the child to understand how tearful he is today: will he cry himself today because the compote is tasteless, will he burst into tears because Katya and Vanya are already crying, but he is not yet, or will he play with cubes with concentration, not paying attention to the tears and snot of comrades.
Knowing today's tearfulness of each of the children, determine whether today the whole group will sob at the same time, or will do without a mass hysteria.
Input
The first line contains an integer n (1n1000) — the number of children in the group. The next line contains n numbers separated by a space, and the i-th number qi (0qin−1 ) denotes the crying of the i-th child. The number qi indicates the number of children that must cry for this child to cry too. If qi = 0, then this child will definitely cry today just like that, regardless of his comrades. It is believed that a child cannot start crying if the right number of children do not cry around him. If a child starts crying, he will not calm down until the evening.
Imprint
Print "YES" if the whole group will cry at the same time, or "NO" otherwise.
Examples
| # |
Input |
Output |
| 1 |
4
1 0 1 2
| YES |
| 2 |
3
1 1 1
| NO |
| |
![]()
|
|
Темы:
Cycles
Yegor loves Moscow very much and often goes for a walk to admire its views.
Moscow in Egor's view is a long straight highway, along which there are n towers, numbered in their order from 1 to n. All towers have different heights, which are expressed as integers from 1 to n . The height of tower i is hi .
However, Egor does not like increasing sequences. He is disappointed with triplets of towers, such that as their indices increase, their values also increase. More formally, the triple of towers numbered i , j and k disappoints Egor if i < j < k and hi < hj < h k .
Egor knows the heights of all the towers in Moscow in advance and wants to know if he will be very disappointed on a walk. Help him determine how many tower triplets he will be disappointed with.
Input
The first line of the input contains a single number n — number of towers in Moscow ( 1 ≤ n ≤ 8000 ).
The second line of the input contains n distinct natural numbers, the i -th of them h i — height of i -th tower ( 1 ≤ hi ≤ n ).
Imprint
Print one number — the number of triples of towers that will disappoint Egor.
Note that the response may not fit in the standard 32-bit data type. It is necessary to use a 64-bit type, in pascal it is called « int64 ", in C++ " long long ", in Java " long».
Examples
| # |
Input |
Output |
| 1 |
5
1 3 4 2 5
| 5 |
| 2 |
3
3 1 2
| 0 |
| |
![]()
|
|
Темы:
One-Dimensional Arrays
Cycles
10 buildings were built in a row on Novy Prospekt. Each building can be either a residential building, or a shop, or an office building.
But it turned out that the residents of some houses on Novy Prospekt had to walk too far to get to the nearest store. To develop a plan for the development of public transport on Novy Prospekt, the mayor of the city asked you to find out what is the greatest distance residents of Novy Prospekt have to travel to get from their homes to the nearest store.
Input
The program receives ten numbers as input, separated by spaces. Each number specifies the type of building on Novy Prospekt: number 1 indicates a residential building, number 2 indicates a store, number 0 indicates an office building. It is guaranteed that there is at least one residential building and at least one shop on Novy Prospekt.
Imprint
Print a single integer: the maximum distance from the house to the nearest store. The distance between two neighboring houses is considered equal to 1 (that is, if two houses are side by side, then the distance between them is 1, if there is another house between two houses, then the distance between them is 2, etc.)
Examples
| # |
Input |
Output |
Explanation |
| 1 |
2 0 1 1 0 1 0 2 1 2 |
3 |
In the example from the condition, residents of the fourth house have the furthest to go to the nearest store: the nearest store to their house is in the first house, and they need to walk three houses to it. Residents of other houses will have to walk a shorter distance to the nearest store, so the answer is 3. |
| |
![]()
|
|
Темы:
while loop
One-Dimensional Arrays
Cycles
We all know that the winter that has begun will end soon, and everyone will eat pancakes during the Maslenitsa celebration. This will be our task.
N guests are seated at a table, and each has a plate of pancakes in front of them. There are ai pancakes on the plate of the i-th guest. Each guest eats one pancake in one minute, so the time when the last person finishes eating pancakes is equal to the largest value of ai.
Suddenly, another person joined them, and now all those present can shift some of their pancakes (including they can shift all their pancakes, or they may not shift a single pancake) to the newly arrived person. Pancakes are shifted simultaneously and instantly.
The guests want to shift the pancakes in such a way that after shifting they will eat all the pancakes in the minimum time (which is equal to the largest number of pancakes on the guests' plates, including the new guest). Determine the shortest time in which guests can eat their pancakes after being moved.
The program receives as input a natural number N, not exceeding 100.000, – initial number of guests. The next N lines contain natural numbers ai – the number of pancakes on the plate of the i-th person. The values ai are given in non-decreasing order, i.e. ai ≤ ai+1. The sum of the values of all ai does not exceed 2·109.
The program should output a single integer – the minimum time for all guests to finish eating their pancakes after transferring some of the pancakes to the new guest's plate.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4
1
3
5
6 |
4 |
4 people are sitting at the table, they have 1, 3, 5, 6 pancakes on their plates. The last guest will give 2 pancakes to the new guest, and the penultimate – 1 pancake, and then everyone, including the new guest, will have no more than 4 pancakes. |
| |
![]()
|
|
Темы:
Cycles
Gromozeka is about to take part in the final round of the STCoder Contest. In this challenge N the problems are numbered from 1 to N. Gromozeka knows what i problem solution (\(1<=i<=N\)) requires Ti seconds. In addition, participants are offered M types of drinks, numbered from 1 to M. If Gromozeka drinks i (\(1 <= i <= M\)), his brain will be stimulated and time, he needs to solve the Pi problem becomes Xi seconds. This does not affect the time to complete other tasks.
The participant is allowed to drink exactly one of the drinks before the start of the competition. For each drink, Gromozeka wants to know how many seconds it will take him to solve all the problems if he drinks this drink. Suppose that the time it takes him to solve all the problems is equal to the sum of the time needed to solve the individual problems. Your task is to write a time calculation program instead of Gromozeka.
Input
The input is integers. In the first line the number N (\(1<=N<=100\)), in the second line N > numbers Ti (\(1<=T_i<=10^5\)). The third line contains the number M (\(1<=M<=100\)). Next comes M lines, each of which contains a pair of Pi,Xi (\(1<=P_i<=N\), \(1<=X_i<=10^5\) ).
Imprint
For each drink, calculate how many seconds it will take Gromozeka to solve all the problems if he drinks this drink, and print the results, one per line.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
3
2 1 4
2
1 1
2 3
| 6
9 |
If Gromozeka drinks drink number 1, the time it takes him to complete each task will be 1, 1, and 4 seconds, respectively, for a total of 6 seconds.
If Gromozeka drinks drink 2, the time it takes him to complete each task will be 2, 3, and 4 seconds, respectively, for a total of 9 seconds. |
| 2 |
5
7 2 3 8 5
3
4 2
17
4 13 |
19
25
30 |
|
| |
![]()
|
|
Темы:
Cycles
Nested Loops
You are given two integers K and S. Three variables X, Y and Z< /code> take integer values that satisfy the condition \(0<=X,Y,Z<=K\). How many distinct X values are there , Y and Z such that \(X+Y+Z=S\) ?
Input
The input is two integers K (\(2<=K<=2500\)) and S < /code>(\(0<=S<=3\cdot K\)).
Imprint
Print the number of X, Y and Z triples that satisfy the condition.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
2 2 |
6 |
There are six triplets X, Y and Z that satisfy the condition:
X=0, Y=0, Z=2
X=0, Y=2, Z=0
X=2, Y=0, Z=0
X=0, Y=1, Z=1
X=1, Y=0, Z=1
X=1, Y=1, Z=0 |
| 2 |
5 15 |
1 |
Only one triple satisfies the condition of the problem:
X=5, Y=5, Z=5 |
| |
![]()
|
|
Темы:
Strings
Cycles
You have an integer variable x. Initially \(x = 0\). Someone gave you a string S of length N, and using that string you performed the following operation N times. In the ith operation, you incremented x by 1 if Si = I, and decrement x by 1 if Si = D. Find the maximum value x takes during operations (including before the first operation and after the last operation).
Input
The first line contains the number N (\(1<=N<=100\)), the second line contains the string S . The length of the N string. The string contains only the characters I and D.
Imprint
Print the maximum x value obtained during the operations.
Examples
| # |
Input |
Output |
| 1 |
5
IDID
|
2
|
| 2 |
7
DDIDDII
|
0
|
| |
![]()
|
|
Темы:
for loop
Cycles
In some village there are 999 towers 1, (1 + 2), (1 + 2 + 3), ..., (1 + 2 + 3 + ... + 999) meters high from west to east. The distance between two adjacent towers is 1 meter. It snowed for a while before it finally stopped. For two neighboring towers located 1 meter apart, we measured the lengths of the parts of these towers that are not covered with snow and got a meters for the west tower and b meters for the east tower. Assuming that the thickness of the snow cover and the height above sea level are the same in the entire settlement, find the total depth of the snow cover. Let's also assume that the depth of the snow cover is always at least 1 meter.
Input
The input string contains two integers a and b (\(1\leq a<b<499500=1+2+3+...+999\)) . All input data satisfies the condition of the problem.
Imprint
Print the depth of the snow cover.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
8 13 |
2 |
The two towers are 10 meters and 15 meters respectively. Thus, we see that the depth of the snow cover is 2 meters. |
| 2 |
54 65 |
1 |
|
| |
![]()
|
|
Темы:
Whole numbers
Cycles
Nested Loops
Before the celebration of the Day of the programmer, the office of the IT company was decorated with a sequence of numbers of length N, a = {a1, a2, a3, ..., aN}. Bugs Hunter, a member of the testing department, would like to play around with this sequence. In particular, he would like to repeat the following operation as many times as possible.
For every i that satisfies 1<=i<=N, do one of the following: "divide ai by 2" and "multiply ai by 3". You can't do "multiply ai by 3" immediately for each i during one operation, the value of ai after any action must be an integer.
Bugs Hunter does one operation in 1 second, regardless of the number of numbers in the sequence. Determine the maximum time after which Bugs Hunter will return to his work?
Input
The first line contains an integer N (1<=N<=10000). The second line contains N integers ai (1<=ai<=109).
Imprint
Print one number - the maximum number of seconds after which Bugs Hunter will return to his job.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
3
5 2 4
| 3 |
The sequence is originally 5,2,4.
Three operations can be performed as follows:
- first multiply a1 by 3, multiply a2 by 3 and divide a3 by 2. Now the sequence is 15,6,2;
- then multiply a1 by 3, divide a2 by 2 and multiply a3 by 3. Now the sequence is 45,3,6;
- finally multiply a1 by 3, multiply a2 by 3 and divide a3 by 2. Now the sequence is 135,9,3.
Further, with each number, you can only perform multiplication by 3, but this action is not allowed for all numbers ai at once.
So the answer is 3. |
| 2 |
4
631 577 243 199
| 0 |
|
| 3 |
10
2184 2126 1721 1800 1024 2528 3360 1945 1280 1776 |
39 |
|
| |
![]()
|
|
Темы:
Whole numbers
Cycles
For integers b ( b >= 2 ) and n ( n >= 1 ) let the function f(b, n) be defined as follows:
\(f (b, n) = n when\ n < b \\
f (b, n) = f (b, floor (n / b)) + (n \ mod \ b) when \ n >= b\)
Here
floor(n / b) denotes the largest integer not greater than n / b;
n mod b denotes the remainder of n divided by b.
Less formally, f(b, n) is equal to the sum of the n digits in base b. For example, the following is true:
\(f (10.87654) = 8 + 7 + 6 + 5 + 4 = 30\\
f (100.87654) = 8 + 76 + 54 = 138\)
You are given the integers n and s. Determine if there is an integer b (b >= 2) such that f(b, n) = s. If the answer is yes, find the smallest of these b.
Input
The first line contains an integer n (1 <= n <= 1011). The second line contains an integer s (1 <= s <= 1011).
Imprint
Output the answer to the problem. If there is no answer, then print -1.
Examples
| # |
Input |
Output |
| 1 |
87654
30 |
10 |
| 2 |
87654
138 |
100 |
| 3 |
87654
45678 |
-1 |
| 4 |
31415926535
1 |
31415926535 |
| 5 |
1
31415926535 |
-1 |
| |
![]()
|
|
Темы:
Cycles
Arrays
Gromozeka has the following two personal principles: he never travels more than L in one day. He never sleeps outdoors. That is, he must be at the hotel at the end of the day.
The Planet Blue has N hotels and all are located on the same street. The coordinate of the ith hotel (1<=i<=N) is xi.
Traveling around the planet Bluk, Gromozeka planned Q moves. With each move he plans to change hotel aj to bj (1<=j<= Q). For each move, find the minimum number of days Gromozeka needs to get from the ajth hotel to the bjth, following his principles.
It is guaranteed that he can always travel from the ajth hotel to the bjth th hotel.< br />
Input
The first line contains an integer N (2<=N<=105) - the number of hotels on the planet Bluk. The second line contains N numbers xi - coordinates of the i-th hotel (1<=x1<x2< /sub><...<xN<=109 , xi+1−x i<=L). The third line contains the number L (1<=L<=109). The fourth line contains the number Q (1<=N<=105).
The last Q lines contain two different numbers aj and bj (1<=aj,bj<=N). All numbers are integers.
Imprint
Print Q lines. The j-th line (1<=j<=Q) should contain the minimum number of days Gromozeka needs to get from aj-th hotel to bj-th hotel.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
9
1 3 6 13 15 18 19 29 31
10
4
18
7 3
67
8 5 |
4
2
1
2 |
On the 1st crossing, he can travel from the 1st hotel to the 8th in 4 days as follows:
Day 1: Transfer from the 1st hotel to the 2nd hotel. Distance traveled - 2.
Day 2: Transfer from the 2nd hotel to the 4th. Distance traveled - 10.
Day 3: Transfer from the 4th hotel to the 7th. Distance traveled - 6.
Day 4: Transfer from the 7th hotel to the 8th. Distance traveled - 10. |
| |
![]()
|
ID 38749.
Vote
Темы:
Cycles
Constructive
Case Study
The shorties decided to take Dunno or Donut on a flight to the moon. Unable to reach an agreement, they decided to vote. Dunno and Donut watch the voting summary. The Shorties show Dunno and Donut the ratio of the current number of votes received by Dunno and Donut, but not the actual number of votes. Dunno and Donut looked at the report N times, and when they looked at it the i (1<=i<=N) times, the ratio was Pi:Ni. Dunno and Donut are known to have had at least one vote when they first saw the report. Find the minimum possible total number of votes Dunno and Donut received when they checked the report for the Nth time. It can be assumed that the number of votes received by Dunno and Donut never decreases.
Input
The first line specifies an integer N (1<=N<=1000). The following N lines contain 2 numbers each Pi and Ni ;(1<=Pi,Ni<=1000). Pi and Ni are relatively prime numbers.
Imprint
Output the minimum possible total number of votes. It is guaranteed that the correct answer is no more than 1018.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
3
23
1 1
3 2 |
10 |
The number of votes received by Donut and Dunno changes as follows: 2.3 → 3.3 → 6.4.
The total number of votes at the end is 10, which is the lowest possible number. |
| 2 |
4
1 1
1 1
15
1 100
| 101 |
It's possible that neither Donut nor Dunno got votes between the time they viewed the report and the next time they viewed it. |
| 3 |
5
3 10
48 17
31 199
231 23
3 2 |
6930 |
|
| |
![]()
|
|
Темы:
Cycles
One day, in a remote lesson via some kind of video conferencing service, the teacher noticed that one of the N students in the class was missing. To understand who exactly is missing, the teacher asked each student present to write in the chat his number in the class journal: a number from 1 to N. Then, after the end of the lesson, by viewing the saved chat, the teacher will be able to understand which of the students did not write his number. Help him - write a program that will do it.
Input
The first line of the input contains an integer N (1 <= N <= 105 ) — the number of students in the class. The following N-1 lines contain one number each — the numbers of the students present at the lesson in random order. Among these numbers, every number from 1 to N, except for one, occurs exactly once.
Imprint
The program should output a single number — number of the missing student.
Examples
| # |
Input |
Output |
| 1 |
5
2
5
1
3 |
4 |
| |
![]()
|
|
Темы:
Cycles
In some other world today is December 29th. Daryona and her grandfather Kokovaniy decided to buy N goods at the department store for a fun New Year celebration. The regular price of the ith item (1 <= i <= N) is pi silver pebbles, and p i is always even. Kokovani's grandfather has a discount coupon and can buy one item at the highest price for half the regular price. The remaining N − 1 items are at their regular price. How many times does the Silver Hoof need to be hit so that Darena and her grandfather can pay for the goods? For one hit, one silver pebble flies out from under the hoof.
Input
The first line contains an integer N (2 <= N <= 105). The following N lines contain positive even integers pi (100 <= pi <= 106), each number on a separate line.
Imprint
Display the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
3
4980
7980
6980
|
15950
|
| |
![]()
|
|
Темы:
Cycles
Arrays
In some world, it's December 31st and all the fun is just beginning. Snezhik Sugrobovich made N large snowballs and arranged them in a row from left to right. On each ith snowball, counting from the left (1 <= i <= N ), he wrote the integer ai. He invites you to play a game. Snezhik Sugrobovich allowed to break no more than N − 1 snowballs of your choice.
Let's say there are K snowballs left. Snezhik Sugrobovich will be satisfied and give you a good gift if for each integer i (1<=i<=K) on the i-th snowball, counting the remaining snowballs on the left , an integer will be written i.
Find the minimum number of snowballs you need to break in order to receive a gift. If it doesn't work, then print -1.
Input
In the first line, the program receives an integer N (1 <= N <= 200000) as input. In the second line - N natural numbers ai (1<=ai<=N).
Imprint
Print the minimum number of snowballs that need to be broken to get a present, or print -1 if it's impossible.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
3
2 1 2
| 1 |
Break the first snowball, the numbers on the rest of the snowballs will satisfy Snezhik Sugrobovich's condition |
| 2 |
3
2 2 2
| -1 |
|
| 3 |
10
3 1 4 1 5 9 2 6 5 3
| 7 |
|
| 4 |
1
1 |
0 |
|
| |
![]()
|
|
Темы:
Cycles
Combinatorics
Snezhik Sugrobovich put a row of N Christmas balls in order to color them. He decided that each ball would be one of K colors. At the same time, Snezhik Sugrobovich wants any two adjacent Christmas tree balls & nbsp; were painted in different colors. Find the number of possible ways to color the Christmas balls.
Input
The input string contains two integers N and K (\(1<=N<=1000\), \(2<=K<=1000\)).
Imprint
Display the answer to the problem. It is guaranteed that the correct answer does not exceed \(2^{31}-1\).
Examples
| # |
Input |
Output |
| 1 |
2 2 |
2 |
| 1 |
1 10 |
10 |
| |
![]()
|
|
Темы:
Cycles
Given a monotonic sequence in which each natural number k occurs exactly k times: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, ...
Given a natural n print the first n members of this sequence. Only one loop is allowed per task.
Input
Enter a natural number n.
Imprint
Print the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
2 |
1 2 |
| 2 |
5 |
1 2 2 3 3 |
| |
![]()
|
|
Темы:
Cycles
Implementation task
A broken color printer, printing numbers, paints all enclosed areas red. For example, the numbers 0, 4, 6, 9 have one closed area. In the figure 8 - 2 closed areas. In other numbers, there are no closed areas that are painted over. There are h closed areas remaining in the red printer for painting. Find the minimum non-negative number that will print out the red ink in the printer. The number must not contain leading zeros. If the printer is out of red ink, it cannot print a closed area number.
Input
The input is a number h (0 <= h <= 510).
Imprint
Output the number to be printed.
Examples
| # |
Input |
Output |
| 1 |
15 |
48888888 |
| 2 |
70 |
8888888888888888888888888888888888 |
| |
![]()
|
|
Темы:
Cycles
Given a non-empty sequence of integers ending in zero. Zero is not included in the sequence, it serves as a sign of its end. Determine the average value of all elements of the sequence.
Input
A sequence of integers is entered, ending with the number 0 (the number 0 itself is not included in the sequence, but serves as a sign of its end).
Imprint
Print the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
4
2
7
0 |
4.333333333333333 |
| |
![]()
|
|
Темы:
Cycles
First grader Fedor likes to add numbers in a column, but only if the examples are easy. He considers easy examples in which it is not necessary to make transfers from the low order to the high ones. All other examples he finds difficult.
You are given positive integers A and B. Count A+B (in decimal). If it doesn't involve a carry in some place, print Easy, otherwise print Hard.
Input
The program takes as input one string containing two integers A and B (1 <= A, B < = 1018).
Imprint
Print the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
229 390 |
Hard |
| 2 |
123456789 9876543210 |
Easy |
| |
![]()
|
|
Темы:
Cycles
Calculate
\(P = (1 + \sin 0.1 ) \cdot (1 + \sin 0.2 ) \cdot ...\cdot (1 + \sin 1 )\)
Input
No.
Imprint
Output number P.
| |
![]()
|
|
Темы:
Cycles
You are given a real number x. Calculate
\(s = {{(x-1)\cdot(x-3)\cdot(x-7)\cdot ...\cdot(x-63)}\over{(x-2)\cdot(x-4)\cdot(x-8)\cdot...\cdot(x-64)}}\)< /span>
Input
A real number x (-50 <= x <= 50) is entered. It is guaranteed that a solution exists for the given x.
Imprint
Print the value S.
| |
![]()
|
|
Темы:
Cycles
Given a natural number N, a real number A. Calculate
\(S = {{1 \over A} + {1 \over {A^2}} + {1 \over A^4} +... + {1 \over A^{2\cdot N - 2}} }\)
Input
The first line contains a natural number N (0 < N <= 10). The second line contains a real number А (- 5 <= A<= 5, A!=0).
Imprint
Output the S. value
| |
![]()
|
|
Темы:
Cycles
Given a natural number N, a real number A. Calculate
\(P = A \cdot (A - N) \cdot (A - 2 \cdot N) \cdot... \cdot (A - N^2)\)
Input
The first line contains a natural number N (0<N<=10). The second line contains a real number A (-10< ;=A<=10).
Imprint
Output number P.
| |
![]()
|
|
Темы:
Cycles
Given a natural number N, a real number A. Calculate
\(P = A \cdot (A + 1) \cdot...\cdot (A + N - 1)\ )
Input
The first line contains a natural number N (0<N<=10). The second line contains a real number A (-100< ;=A<=100).
Imprint
Output number P.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {(-1)^{n-1} \over{n^n}}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {{1\over 2^n} + {1 \over 3^n}}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {{2\cdot n-1} \over{2^n}}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {1 \over{(3 \cdot n - 2)\cdot(3\cdot n+1) }}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {{n!} \over{(2\cdot n)!}}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {n! \over{n^n}}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {2^n \cdot n! \over{n^n}}\)< /div>
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {n! \over{3 \cdot n^n}}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {{n!} \over{(2^n)!}}\)< /div>
Display the sum of such a series.
| |
![]()
|
|
Темы:
Cycles
Given a number series and a small value eps=0.001. With eps precision (that is, if the sum of the next addition of a term differs by less than 0.001 from the previous one, then this term is considered the last one) find the sum of the series whose common term is given by the formula (n>0):
\(a_n = {(2)^{n} \over{(n-1)!}}\)
Display the sum of such a series.
| |
![]()
|
|
Темы:
Implementation task
One-Dimensional Arrays
Cycles
Alice and Gromozeka went for a walk around the city. Entering the first cafe, Alice looked at her watch and remembered the time of entry. Further, she memorized only the number of minutes that she and Gromozeka spent between two cafes visited (from entering one cafe to entering another). At the end of the walk, Alice decided to restore the chronology - the time of entering the next cafe.
Write a program that will determine at what time Alice and Gromozeka went to the next cafe.
Input
The first line specifies the moment of time at which Gromozeka and Alice entered the first cafe. Time format: hours (a number from 00 to 23), followed by a colon, then minutes (a number from 00 to 59). The time string is written without spaces.
The second line contains a natural number N (2 <= N <= 1000) - the number of visited cafes (including the cafe from which they left at the initial moment of time and the last cafe). The third line contains N-1 number: the first one shows the time in minutes from the entrance to the first cafe to the entrance to the second one, the second - the time from the entrance to the second cafe to the entrance to the third one, and so on. Each of these numbers is natural and does not exceed 1000.
Imprint
Print for each cafe the entry time of Alice and Gromozeka. The time format must be the same as in the input data.
Examples
| # |
Input |
Output |
| 1 |
07:00
4
10 5 3
| 07:00
07:10
07:15
07:18 |
| |
![]()
|
|
Темы:
USE
Cycles
Given a sequence of N natural numbers. All its continuous subsequences starting from the first element of the sequence are considered. Find the number of subsequences whose sum is a multiple of K.
Input
The first line contains two numbers: the number of numbers in the sequence N (1 <= N <= 108) and the number K ( 1 <= K <= 100). Next comes N lines, one natural number per line. Each number does not exceed 10000.
Imprint
Display the answer to the problem
Examples
| # |
Input |
Output |
| 1 |
5 3
33
41
19
22
40 |
2 |
| |
![]()
|
|
Темы:
Cycles
At competitions in chess composition, each participant is given 10 problems to solve. For each task, you can get from 0 to 5 points. For a correctly solved problem, the participant is awarded 5 points. If the problem is not solved completely or not correctly, then the participant is given a second attempt. In this case, for the task, the participant receives a score equal to the average score for two attempts, rounded according to the rules of mathematics.
Points are given in order from the first to the last solved problem.
Little Vitya Ch., participating in his first competition in his life, forgot how many problems he solved. Vitya Ch. remembers that he received only 10 ratings, as well as the ratings themselves in order.
Determine how many problems Vitya Ch. solved in total, how many problems he got the maximum score on the first attempt, and the total amount of points he scored.
Input
The program receives 10 lines, each of which contains one non-negative number from 0 to 5.
Imprint
Print in the first line the number of problems that Vitya Ch. managed to solve, in the second line - the number of problems that he solved on the first attempt for the maximum score, in the third line - the total number of points scored.
Examples
| # |
Input |
Output |
| 1 |
2
5
2
5
0
5
5
2
5
5 |
6
2
25 |
| |
![]()
|
|
Темы:
Cycles
Real numbers
The nutrition of a schoolchild, with proper organization, should provide the content of proteins, fats and carbohydrates in a ratio of 10%: 30%: 60% (an error of +/- 1% is allowed). The children's camp is compiling a menu consisting of N different products. For each product, the energy value in proteins (P), fats (F) and carbohydrates (C), as well as the amount of each type of product in menu(K).
Determine if the menu is balanced or not.
Input
The program receives several lines as input. The first line contains a natural number N (N <= 100) the number of different products. Each of the following N lines contains 4 numbers: Pi, Fi, Ci and Ki. All numbers are real, do not exceed 103.
Imprint
Print YES if the menu is balanced, and NO otherwise.
Examples
| # |
Input |
Output |
| 1 |
3
0 1 1 2
1 2 7 1
3 7 13 1
| YES |
| |
![]()
|
|
Темы:
Cycles
Whole numbers
Gromozeka and Alice are playing the following game. Initially, they put three points on the number line in integer coordinates. Then, one of them erases any extreme point and puts it in the middle between the two remaining ones in a coordinate with an integer. If there is an even number of integers between the remaining points, then you can put a point in any of them.
For example, if initially there were points at coordinates 3, 6, 8, then the first move can be to erase the point with coordinate 3 and put it in coordinate 7. Or erase the point with coordinate 8 and put it in coordinate 4 or 5.
In order not to think for a long time, Gromozeka and Alice decided that they would spend no more than two seconds on each move.
You will be asked to calculate the maximum number of seconds the game will last if the starting positions of the three dots are known.
Input
The program takes as input three integers A, B and C (1<=A < B < C <= 1000). Each number is written on a new line.
Imprint
Print the answer to the problem.
Examples
| |
![]()
|
|
Темы:
Cycles
while loop
The performer “Aquarius” there are two vessels, the first with a volume of A liters, the second with a volume of B liters, as well as a tap with water. Aquarius can perform the following operations:
- Fill vessel A (indicated by >A).
- Fill vessel B (indicated by >B).
- Pour water out of vessel A (denoted by A>).
- Pour water out of vessel B (denoted by B>).
- Pour water from vessel A into vessel B (denoted as A>B).
- Pour water from vessel B into vessel A (denoted as B>A).
The command to pour from one vessel to another results in either the first vessel being completely emptied or the second vessel being completely filled.
Input
The program receives as input three natural numbers A, B, N not exceeding 104.
Output
It is necessary to display the Aquarius action algorithm, which allows you to get exactly N liters in one of the vessels, but if such an algorithm does not exist, then the program should display the text Impossible.< /p>
The number of operations in the algorithm should not exceed 105. It is guaranteed that if the problem has a solution, then there is a solution that contains no more than 105 operations.
Examples
| # |
Input |
Output |
| 1 |
3
5
1
|
>A
A>B
>A
A>B
|
| 2 |
3
5
6
|
Impossible
|
| |
![]()
|
|
Темы:
Cycles
Arithmetic Algorithms
Today the boy Sasha learned about fractals at a mathematics lesson. The teacher showed the so-called "dragon curve". It is a geometric figure, which is constructed as follows: at the first step, a segment is drawn from the origin of the coordinate plane to the point (0; 1). Further, at each step from the end of the fractal, the already drawn part of the figure is repeated, rotated 90 degrees counterclockwise (see figure).

After the lessons, Sasha tried to draw the "dragon curve" himself, and now he wants to know at what point on the coordinate plane he finished drawing the fractal by following the N steps described above. It is required to write a program that, given the number of N determines the coordinates of the end of the fractal after performing N steps.
Input
A single integer is entered N (1 <= N <= 30).
Imprint
Output two space-separated numbers - the coordinates of the end of the fractal.
Examples
| # |
Input |
Output |
| 1 |
2 |
1 1 |
| 2 |
4 |
2 -2 |
| |
![]()
|
|
Темы:
Cycles
Professor Seleznev analyzes signals from space. It logs the signal intensity every second as an integer. He does this until the signal fades. Therefore, each record of his observations ends with the number 0. Now he would like to know the maximum time duration of a signal of the same intensity. Seleznev can observe signals for quite a long period of time and it will be quite difficult for him to manually calculate the maximum duration of such a signal. Help him determine this time period.
Input
The input to the program is integers, one number per line. The last line contains the number 0. (Number 0 - sign of its end).
Imprint
The maximum duration in seconds of a signal of the same intensity.
Examples
| # |
Input |
Output |
| 1 |
2
2
2
3
3
1
1
1
1
0 |
4 |
| |
![]()
|
|
Темы:
for loop
Cycles
Simple puzzles
Implementation task
Gromozeka loves valerian very much. On his home planet Chumaroza you can buy for k chumriks (local currency) the first package of valerian, for 2·k chumriks - the second and so on (in other words, ith packing you have to pay i·k chumrikov). Gromozek wants to buy w packages of valerian. He has n chumriks. How many chumriks will he have to take on credit from the chumaroz bank in order to buy w packages of valerian?
Input
The first line contains three positive integers k, n, w (1 <= k, w< /code> <= 1000, 0 <= n <= 109) , the cost of the first package, Gromozeka's initial number of chumaroziki and the number of packages of valerian he wants to buy.
Output
Print a single integer - the number of chumaroziks that Gromozeka needs to borrow from the bank. If you don't need to take a loan, print 0.
Examples
| # |
Input |
Output |
| 1 |
3 17 4 |
13 |
| |
![]()
|